Sortieren ist eine der am häufigsten verwendeten Funktionen in der Programmierung. Und es dauert, bis die Sortierung abgeschlossen ist, wenn wir nicht den richtigen Algorithmus verwendet haben.
In diesem Artikel werden wir verschiedene Sortieralgorithmen besprechen.
Wir werden Sie durch die verschiedenen Sortieralgorithmen führen, mit jedem Schritt, der zur Implementierung gehört. Der Teil der Implementierung erfolgt in Python. Sobald Sie den Algorithmus verstanden haben, können Sie ihn leicht in jede beliebige Sprache konvertieren. Das ist eine Frage der Sprachsyntax.
In diesem Tutorial werden wir verschiedene Algorithmen von der schlechtesten bis zur besten Variante sehen. Machen Sie sich also keine Sorgen. Folgen Sie dem Artikel und implementieren Sie sie.
Lassen Sie uns in die Sortieralgorithmen eintauchen.
Einfügungs-Sortierung
Die Einfügesortierung ist einer der einfachsten Sortieralgorithmen. Er ist leicht zu implementieren. Und es kostet Sie mehr Zeit, ein Array zu sortieren. Er wird in den meisten Fällen nicht zum Sortieren größerer Arrays verwendet.
Der Algorithmus für die Einfügesortierung verwaltet sortierte und unsortierte Unterbereiche in dem gegebenen Array.
Der sortierte Unterteil enthält nur das erste Element zu Beginn des Sortiervorgangs. Wir nehmen ein Element aus dem unsortierten Array und platzieren es an der richtigen Stelle im sortierten Unterarray.
Lassen Sie uns die visuellen Illustrationen der Einfügungssortierung Schritt für Schritt anhand eines Beispiels betrachten.
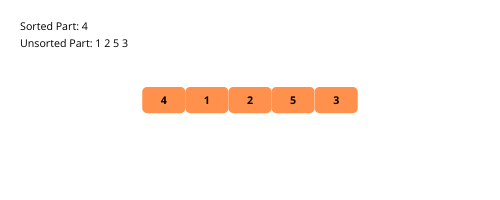
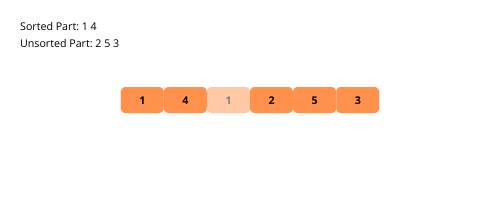
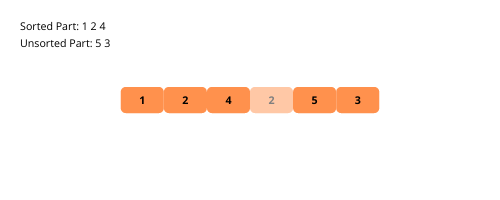
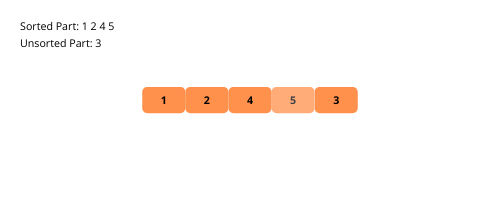
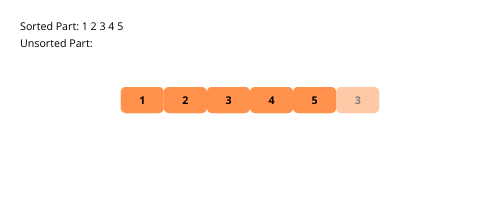
Sehen wir uns die Schritte zur Implementierung der Einfügesortierung an.
- Initialisieren Sie das Array mit Dummy-Daten (Ganzzahlen).
- Iterieren Sie über das gegebene Array ab dem zweiten Element.
- Nehmen Sie die aktuelle Position und das Element in zwei Variablen auf.
- Schreiben Sie eine Schleife, die solange iteriert, bis das erste Element des Arrays oder das Element auftritt, das kleiner ist als das aktuelle Element.
- Aktualisieren Sie das aktuelle Element durch das vorherige Element.
- Dekrementieren Sie die aktuelle Position.
- Hier muss die Schleife entweder den Anfang des Arrays erreichen oder ein kleineres Element als das aktuelle Element finden. Ersetzen Sie das Element der aktuellen Position durch das aktuelle Element.
Die Zeitkomplexität der Einfügesortierung ist O(n^2) und die Raumkomplexität O(1).
Das war’s. Wir haben das gegebene Array sortiert. Lassen Sie uns den folgenden Code ausführen. Ich hoffe, Sie haben Python installiert. Falls nicht, sehen Sie sich die Installationsanleitung an. Alternativ können Sie auch einen Online-Python-Compiler verwenden.
def insertion_sort(arr, n):
for i in range(1, n):
## aktuelle Position und Element
aktuelle_position = i
aktuelles_element = arr<x><x><x><x><x>[i]</x></x></x></x></x>
## Iteration bis
### das erste Element erreicht ist oder
### das aktuelle Element kleiner ist als das vorherige Element
while aktuelle_position > 0 und aktuelles_element <
arr[aktuelle_position - 1]:
## Aktualisieren des aktuellen Elements mit dem vorherigen Element
arr<x>[aktuelle_Position]</x> = arr[aktuelle_Position - 1]
## Verschieben zur vorherigen Position
aktuelle_Position -= 1
## Aktualisieren des Elements mit der aktuellen Position
arr<x>[aktuelle_Position]</x> = aktuelles_Element
if __name__ == '__main__':
## Initialisierung des Arrays
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
einfügen_sortieren(arr, 9)
## Drucken des Arrays
print(str(arr))Auswahl sortieren
Die Auswahlsortierung ist ähnlich wie die Einfügesortierung mit einem kleinen Unterschied. Auch bei diesem Algorithmus wird das Array in sortierte und unsortierte Unterteile aufgeteilt. Und dann nehmen wir bei jeder Iteration das kleinste Element aus dem unsortierten Teilbereich und setzen es an die letzte Position des sortierten Teilbereichs.
Sehen wir uns zum besseren Verständnis die Illustrationen der Auswahlsortierung an.
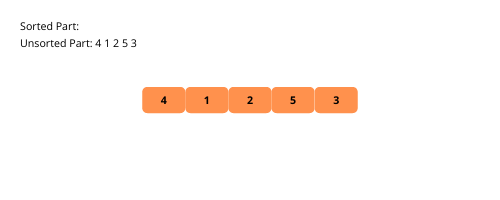
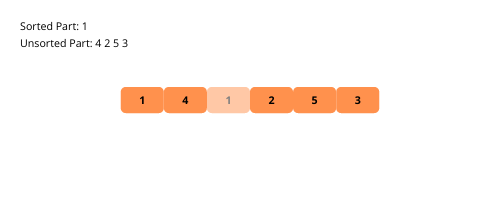
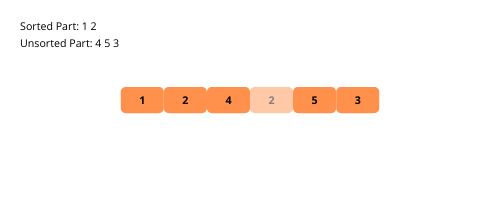
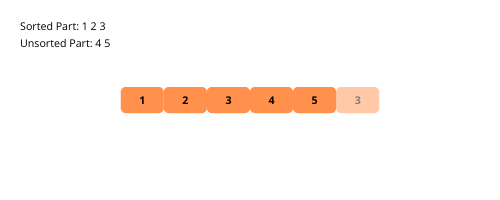
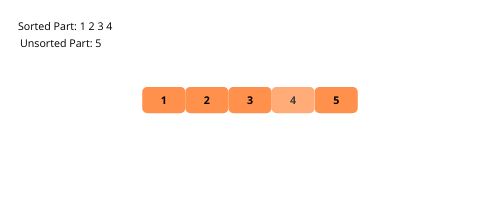
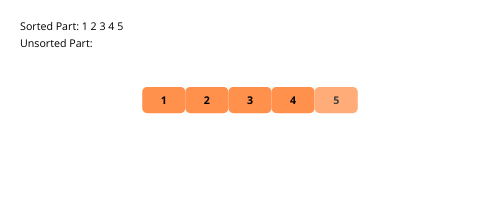
Sehen wir uns die Schritte zur Implementierung der Auswahlsortierung an.
- Initialisieren Sie das Array mit Dummy-Daten (Ganzzahlen).
- Iterieren Sie über das gegebene Array.
- Behalten Sie den Index des kleinsten Elements bei.
- Schreiben Sie eine Schleife, die vom aktuellen Element bis zum letzten Element iteriert.
- Prüfen Sie, ob das aktuelle Element kleiner als das Mindestelement ist oder nicht.
- Wenn das aktuelle Element kleiner als das minimale Element ist, dann ersetzen Sie den Index.
- Wir haben den Index des minimalen Elements dabei. Tauschen Sie das aktuelle Element mit dem Mindestelement unter Verwendung der Indizes aus.
Die Zeitkomplexität der Auswahlsortierung ist O(n^2) und die Raumkomplexität ist O(1).
Versuchen Sie, den Algorithmus zu implementieren, da er der Einfügesortierung ähnelt. Sie können den Code unten sehen.
def selection_sort(arr, n):
for i in range(n):
## um den Index des kleinsten Elements zu speichern
min_element_index = i
for j in range(i 1, n):
## Prüfen und Ersetzen des Index des minimalen Elements
if arr<x><x><x><x><x>[j]</x></x></x></x></x> < arr<x><x>[min_element_index]</x></x>:
min_element_index = j
## Vertauschen des aktuellen Elements mit dem minimalen Element
arr<x><x><x><x><x>[i]</x></x></x></x></x>, arr<x><x>[min_element_index]</x></x> = arr<x><x>[min_element_index]</x></x>, arr<x><x><x><x><x>[i]</x></x></x></x></x>
if __name__ == '__main__':
## Array-Initialisierung
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
auswahl_sort(arr, 9)
## Drucken des Arrays
print(str(arr))Blasen-Sortierung
Bubble Sort ist ein einfacher Algorithmus. Er vertauscht bei jeder Iteration wiederholt die benachbarten Elemente, bis das gegebene Array sortiert ist.
Er durchläuft das Array und verschiebt das aktuelle Element an die nächste Position, bis es kleiner als das nächste Element ist.
Illustrationen helfen uns, die Bubble-Sortierung visuell zu verstehen. Lassen Sie uns diese sehen.
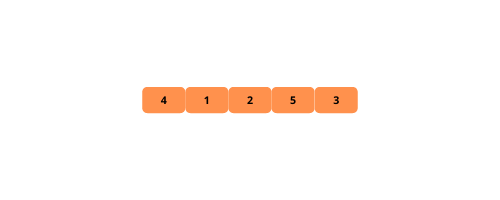
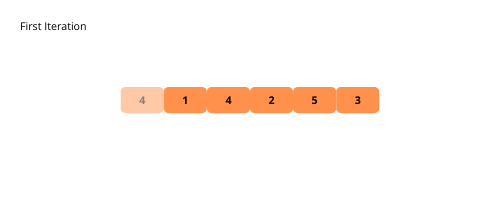
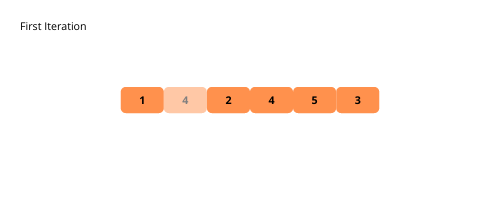

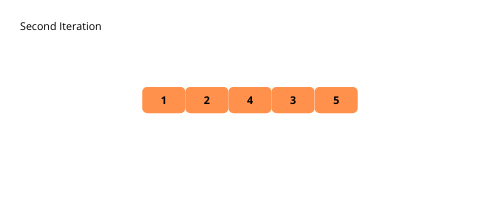
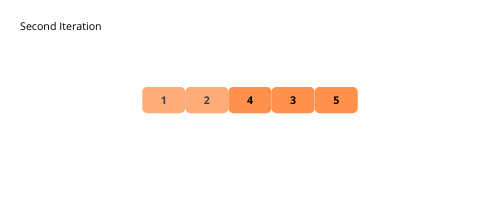
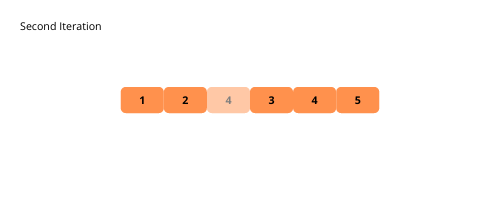
Sehen wir uns die Schritte zur Implementierung der Blasensortierung an.
- Initialisieren Sie das Array mit Dummy-Daten (Ganzzahlen).
- Iterieren Sie über das gegebene Array.
- Iterieren Sie von 0 bis n-i-1. Die letzten i Elemente sind bereits sortiert.
- Prüfen Sie, ob das aktuelle Element größer ist als das nächste Element oder nicht.
- Wenn das aktuelle Element größer als das nächste Element ist, dann tauschen Sie die beiden Elemente aus.
- Iterieren Sie von 0 bis n-i-1. Die letzten i Elemente sind bereits sortiert.
Die Zeitkomplexität der Bubble-Sortierung ist O(n^2), und die Raumkomplexität ist O(1).
Sie können die Bubble-Sortierung jetzt ganz einfach implementieren. Sehen wir uns den Code an.
def bubble_sort(arr, n):
for i in range(n):
## iteriert von 0 bis n-i-1, da die letzten i Elemente bereits sortiert sind
for j in bereich(n - i - 1):
## Prüfen des nächsten Elements
if arr<x><x><x><x><x>[j]</x></x></x></x></x> > arr[j 1]:
## Vertauschen der benachbarten Elemente
arr<x><x><x><x><x>[j]</x></x></x></x></x>, arr[j 1] = arr[j 1], arr<x><x><x><x><x>[j]</x></x></x></x></x>
if __name__ == '__main__':
## Initialisierung des Arrays
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
bubble_sort(arr, 9)
## Drucken des Arrays
print(str(arr))Sortieren zusammenführen
Merge Sort ist ein rekursiver Algorithmus zum Sortieren des gegebenen Arrays. Er ist in Bezug auf die Zeitkomplexität effizienter als die zuvor besprochenen Algorithmen. Er folgt dem Ansatz “Teilen und Erobern”.
Der Merge-Sort-Algorithmus teilt das Array in zwei Hälften und sortiert diese getrennt. Nachdem er die beiden Hälften des Arrays sortiert hat, fügt er sie zu einem einzigen sortierten Array zusammen.
Da es sich um einen rekursiven Algorithmus handelt, wird das Array so lange geteilt, bis das Array das einfachste (Array mit einem Element) ist, das sortiert werden kann.
Es ist Zeit für eine Illustration. Schauen wir es uns an.
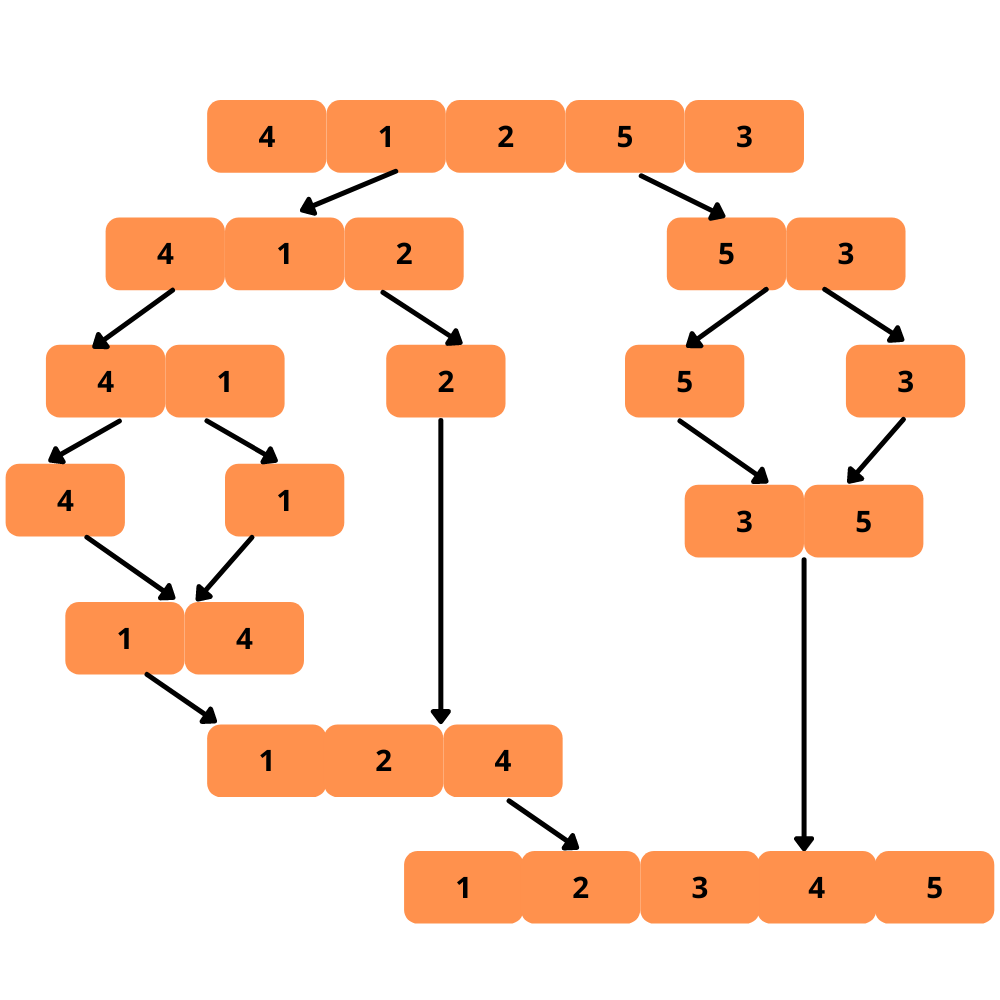
Sehen wir uns die Schritte zur Implementierung der Mischsortierung an.
- Initialisieren Sie das Array mit Dummy-Daten (Ganzzahlen).
- Schreiben Sie eine Funktion namens merge , um die Unter-Arrays zu einem einzigen sortierten Array zusammenzuführen. Sie akzeptiert die Argumente array, left, mid und right indexes.
- Ermitteln Sie die Längen der linken und rechten Sub-Arrays anhand der angegebenen Indizes.
- Kopieren Sie die Elemente aus dem Array in die entsprechenden linken und rechten Arrays.
- Iterieren Sie über die beiden Unter-Arrays.
- Vergleichen Sie die Elemente der beiden Sub-Arrays.
- Ersetzen Sie das Array-Element durch das kleinere Element aus den beiden Sub-Arrays für die Sortierung.
- Prüfen Sie, ob in den beiden Sub-Arrays noch Elemente vorhanden sind.
- Fügen Sie sie dem Array hinzu.
- Schreiben Sie eine Funktion namens merge_sort mit den Parametern array, left und right indexes.
- Wenn der linke Index größer oder gleich dem rechten Index ist, dann geben Sie zurück.
- Finden Sie den mittleren Punkt des Arrays, um das Array in zwei Hälften zu teilen.
- Rufen Sie merge_sort rekursiv mit den Indizes left, right und mid auf.
- Nach den rekursiven Aufrufen führen Sie das Array mit der Funktion merge zusammen.
Die Zeitkomplexität der Zusammenführungssortierung ist O(nlogn) und die Raumkomplexität ist O(1).
Das war’s mit der Implementierung des Merge-Sortieralgorithmus. Sehen Sie sich den Code unten an.
def merge(arr, left_index, mid_index, right_index):
## linke und rechte Arrays
left_array = arr[left_index:mid_index 1]
right_array = arr[mid_index 1:right_index 1]
## Ermitteln der Länge des linken und rechten Arrays
left_array_length = mid_index - left_index 1
right_array_length = right_index - mid_index
## Indizes für das Zusammenführen zweier Arrays
i = j = 0
## Index für die Ersetzung von Array-Elementen
k = linker_index
## Iterieren über die beiden Unter-Arrays
while i < left_array_length und j < right_array_length:
## Vergleich der Elemente aus dem linken und rechten Array
if left_array<x><x><x><x><x>[i]</x></x></x></x></x> < right_array<x><x><x><x><x>[j]</x></x></x></x></x>:
arr<x><x>[k]</x></x> = left_array<x><x><x><x><x>[i]</x></x></x></x></x>
i = 1
sonst:
arr<x><x>[k]</x></x> = right_array<x><x><x><x><x>[j]</x></x></x></x></x>
j = 1
k = 1
## Hinzufügen der verbleibenden Elemente aus den linken und rechten Arrays
while i < left_array_length:
arr<x><x>[k]</x></x> = left_array<x><x><x><x><x>[i]</x></x></x></x></x>
i = 1
k = 1
while j < right_array_length:
j = 1
k = 1
def merge_sort(arr, left_index, right_index):
## Basisfall für rekursive Funktion
if left_index >= right_index:
return
## Ermitteln des mittleren Index
mittlerer_index = (linker_index rechter_index) // 2
## rekursive Aufrufe
merge_sort(arr, linker_index, mittlerer_index)
merge_sort(arr, mitte_index 1, rechts_index)
## Zusammenführen der beiden Unter-Arrays
zusammenführen(arr, linker_index, mittlerer_index, rechter_index)
if __name__ == '__main__':
## Initialisierung des Arrays
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
merge_sort(arr, 0, 8)
## Drucken des Arrays
print(str(arr))Schlussfolgerung
Es gibt noch viele andere Sortieralgorithmen, aber die oben genannten sind einige der am häufigsten verwendeten. Ich hoffe, Sie hatten Spaß beim Lernen der Sortierung.
Als nächstes erfahren Sie mehr über Suchalgorithmen.
Viel Spaß beim Programmieren 🙂 👨💻

