El porcentaje de error en una recopilación de datos es la diferencia entre los valores exactos y aproximados en comparación con el valor original. Este porcentaje de error se expresa como porcentaje y, por tanto, se multiplica por 100.
Puede expresar el porcentaje de error como error absoluto o error relativo. Los errores pueden deberse a un error de precisión en una máquina, a un error de cálculo, a un error de medición o a las condiciones ambientales.
Los errores porcentuales nos ayudan a determinar la importancia de nuestros errores durante cualquier análisis. Los errores porcentuales más leves significan que nos acercamos al valor original, mientras que los errores porcentuales más importantes suponen una discrepancia considerable entre el valor real y el valor aproximado.
Por ejemplo, un error del 2% significaría que estamos muy cerca del valor original, mientras que un error del 56% significaría una diferencia enorme entre el valor real y el aproximado.
Los errores al medir son omnipresentes porque las manos pueden temblar durante las mediciones, los instrumentos pueden estar defectuosos, el material puede no ser preciso, etc.
Cálculo del porcentaje de error
Para calcular el porcentaje de error, debe disponer de dos valores. Uno es el valor exacto y el segundo es el valor aproximado. Reste estos dos valores y luego divídalos por el valor original. Dado que el porcentaje de error se expresa en forma de porcentaje, multiplique el número así obtenido por 100. En otras palabras, el porcentaje de error es el error relativo multiplicado por 100.
Porcentaje de error = [(Valor real – Valor esperado) / Valor esperado] × 100
Componentes de la fórmula
Valor real: El valor real indica el valor numérico de una lectura concreta. El valor real debería haberse registrado al tomar la lectura, pero debido a algunos errores, no pudimos registrar este valor. Es un valor común ideal para realizar cálculos.
Valor esperado: El valor esperado indica la lectura registrada durante la experimentación. En la mayoría de los casos no es similar al valor real debido a errores. Los errores pueden deberse a un defecto en la máquina, a un error al tomar la lectura o a factores ambientales como el aire o instrumentos rotos y dañados.
Algunos ejemplos
Ejemplo 1
Un chico estaba midiendo el área de un triángulo y, según él, la lectura era de 462 cm2. Sin embargo, el área original del cuadrado es de 465 cm2. Calcule el porcentaje de error.
Solución
Valor del área medida = 462 cm2
Valor del área real = 465 cm2
Cálculo
Diferencia del valor real – valor medido: 465-462 = 3
Por tanto, 3 es el error de medición.
Dividir el error por el valor real – 3/465 = 0,00645
Multiplicar el valor obtenido por 100 – 0,00645 X 100 = 0,64%.
Por lo tanto, el porcentaje de error en el cálculo del área de un triángulo es 0,64%
Ejemplo 2
Suponga que estaba planeando una fiesta y que estimó que asistirían 20 personas a la fiesta, mientras que sólo consiguieron venir 18 personas. Calcule el error porcentual en su estimación.
Solución
El número original de personas previsto = 20
Personas que vinieron = 18
Cálculo
Diferencia valor real – valor final = 20 – 18 = 2
Por lo tanto, 2 es el error
Dividir el error por el valor real – 2/20 = 0,1
Multiplicar el valor por 100 – 0,1 X 100 = 10%
Por lo tanto, el porcentaje de error en la estimación del número de invitados es del 10%.
Ejemplo 3
Supongamos que realiza un experimento para medir el punto de ebullición del agua y, mientras experimenta, obtiene un resultado de 102°C. El punto de congelación real del agua es de 100°C.
Solución
El punto de ebullición real del agua = 100°C
El punto de ebullición registrado del agua = 102°C
Cálculo
La diferencia entre el valor real y el valor calculado = 100 -102 = 2°C (El porcentaje de error nunca puede ser negativo, por lo que sólo lo mantenemos positivo).
Por lo tanto, 2 es el error aquí.
Dividir el error por el valor real – 2/100 = 0,02
Multiplicar el valor obtenido por 100 – 0,02 X 100 = 2%
Por lo tanto, el porcentaje de error en la medición del punto de ebullición del agua es del 2%.
Escenarios del mundo real en los que el porcentaje de error es importante
- El porcentaje de error desempeña un papel importante a la hora de ayudarle a determinar si una tarea concreta que ha realizado ha estado a la altura o no. Le ayuda a señalar sus errores.
- El porcentaje de error puede ser útil en procedimientos de laboratorio y en grandes industrias en las que no cabe el más mínimo error.
- El error porcentual también encuentra su uso cuando tenemos que completar un pedido a granel y no puede haber margen de error en su realización.
- En los laboratorios científicos, el uso del error porcentual es fundamental.
Error porcentual frente a error absoluto
El error absoluto en una medición es la diferencia entre el valor real y el calculado. La unidad del error fundamental es la misma que el valor inicial.
Ejemplo
Supongamos que tenía previsto comprar 2 kg de mangos mientras que el tendero le midió 1,98 kg. El error absoluto, en este caso, será 2 – 1,98 = 0,02.
Por otro lado, el porcentaje de error se calcula dividiendo el error absoluto por el valor original y multiplicando después la respuesta obtenida por 100. El porcentaje de error es una cantidad sin unidades.
En el ejemplo anterior, el error absoluto es 0,02.
Ahora, para calcular el porcentaje de error, lo dividiremos por 20.
0.02/20 = 0.001
El porcentaje de error, en este caso, es por tanto 0,001 X 100 = 0,1%.
Error porcentual frente a error relativo
El error relativo en cualquier cálculo es el error absoluto dividido por el valor real. Esto significa que el porcentaje de error es la diferencia entre el valor verdadero y el valor observado dividido por el valor real.
Ejemplo
La previsión meteorológica esperaba que la temperatura hoy fuera de 38°C. Sin embargo, subió a 42°C.
Primero hallamos la diferencia entre los dos números, es decir, el valor esperado y el valor real.
42° – 38° = 4°C
Ahora, para calcular el error relativo, dividimos este número por el número real, es decir, 38°C
4/38 = 0.1052
Por otro lado, el porcentaje de error es un error relativo multiplicado por 100.
En el ejemplo anterior, el porcentaje de error será 0,1052 X 100 = 10,52%.
Ahora bien, puede que le resulte bastante fácil calcular el error porcentual, el error relativo o el error absoluto.
Puede facilitar el cálculo del porcentaje de error con la ayuda de varias calculadoras de porcentaje de error en línea. Ahora, no tendrá que preguntarse cómo calcular el porcentaje de error porque estas calculadoras pueden hacerlo todo por usted.
Herramientas de cálculo de errores
#1. Sopa de calculadoras
Calculator Sou p le ayuda a calcular el porcentaje de error entre el valor experimental y el valor real. Todo lo que tiene que hacer es introducir los valores y esperar los resultados. La calculadora realiza todos los cálculos por sí misma y le proporciona resultados precisos.
La página muestra dos columnas diferentes en las que usted introduce el valor de los números para los que desea calcular el porcentaje de error y deja que la calculadora haga el resto de la magia.
#2. Calculator.net
Calculator.net tiene dos columnas en las que usted introduce los valores reales y estimados y deja que la calculadora haga el resto de los cálculos. Esto resulta muy útil cuando hay muchas muestras de datos que desea calcular y no tiene tiempo de calcular manualmente el porcentaje de error en cada caso. La calculadora facilita el proceso y le da la respuesta de inmediato sin mucha demora.

Los errores porcentuales son inevitables. Sólo puede reducir su valor, pero no habrá ninguna incidencia cuando la lectura del porcentaje de error llegue a cero. Puede ser aproximadamente cero pero nunca puede ser un cero exacto.
#3. Buenas calculadoras
Muchas calculadoras en línea pueden ayudarle a resolver sus problemas de error porcentual. De ellas, una de las más prácticas es la Calculadora Buena. En esta calculadora, sólo tiene que introducir el valor estimado y el original, y le dará automáticamente los resultados.
Le ahorra la molestia de realizar cálculos exhaustivos y protege su tiempo. Puede resolver rápidamente cálculos exhaustivos en cuestión de segundos y ahorrarle mucho tiempo.
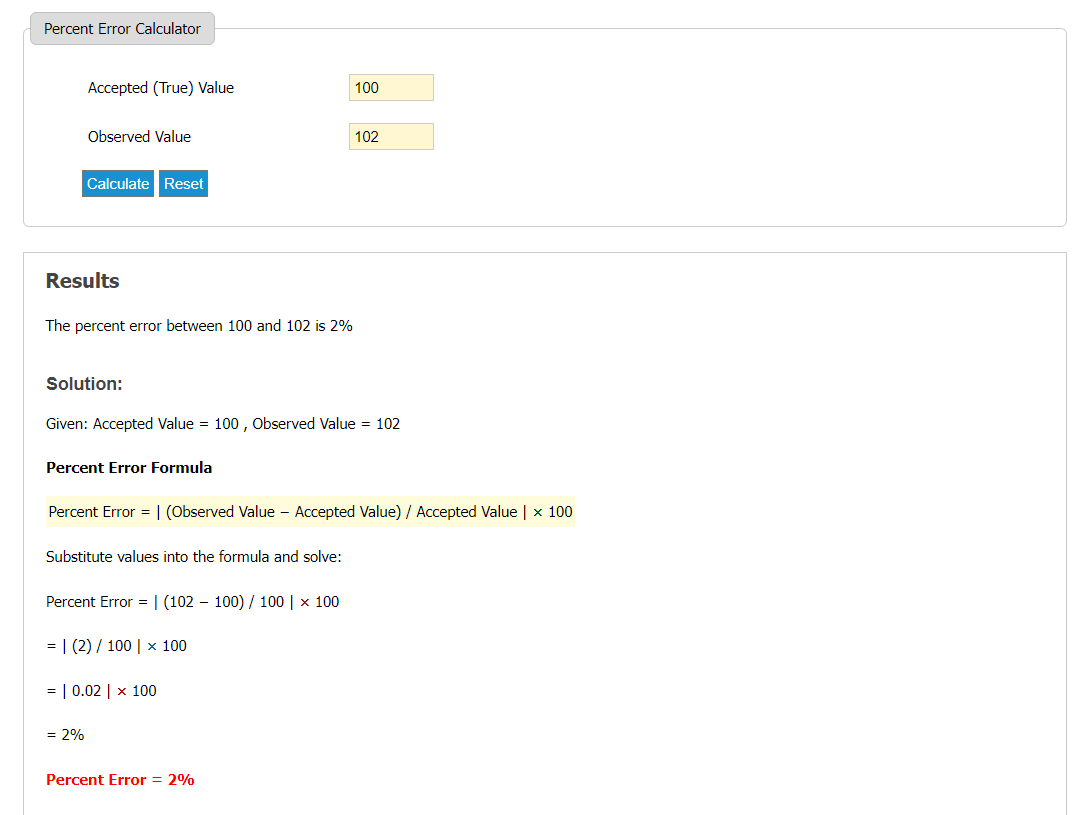
Por lo tanto, una calculadora es ideal para el cálculo del porcentaje de error cuando tiene a mano muchos datos pero le falta tiempo.
Conclusión
Los errores en los cálculos pueden arruinar por completo cualquier proyecto o investigación. Aquí es donde puede recurrir a la ayuda de las calculadoras de porcentaje de error en línea para realizar el trabajo de forma más eficaz y sin errores humanos.
Si lo suyo son las finanzas, puede echar un vistazo a algunas de estas calculadoras de porcentaje de beneficios.

