¿Qué es una matriz de confusión en el aprendizaje automático?

Una matriz de confusión es una herramienta para evaluar el rendimiento del tipo de clasificación de los algoritmos de aprendizaje automático supervisado.

¿Qué es una matriz de confusión?

Los seres humanos percibimos las cosas de forma diferente, incluso la verdad y la mentira. Lo que a mí me puede parecer una línea de 10 cm puede parecerle a usted una línea de 9 cm. Pero el valor real puede ser 9, 10 u otra cosa. Lo que adivinamos es el valor previsto

Al igual que nuestro cerebro aplica nuestra propia lógica para predecir algo, las máquinas aplican varios algoritmos (llamados algoritmos de aprendizaje automático ) para llegar a un valor predicho para una pregunta. Una vez más, estos valores pueden ser iguales o diferentes del valor real.

En un mundo competitivo, nos gustaría saber si nuestra predicción es correcta o no para comprender nuestro rendimiento. Del mismo modo, podemos determinar el rendimiento de un algoritmo de aprendizaje automático por el número de predicciones que hizo correctamente.

Entonces, ¿qué es un algoritmo de aprendizaje automático?

Las máquinas intentan llegar a determinadas respuestas a un problema aplicando cierta lógica o conjunto de instrucciones, denominados algoritmos de aprendizaje automático. Los algoritmos de aprendizaje automático son de tres tipos: supervisados, no supervisados o de refuerzo.

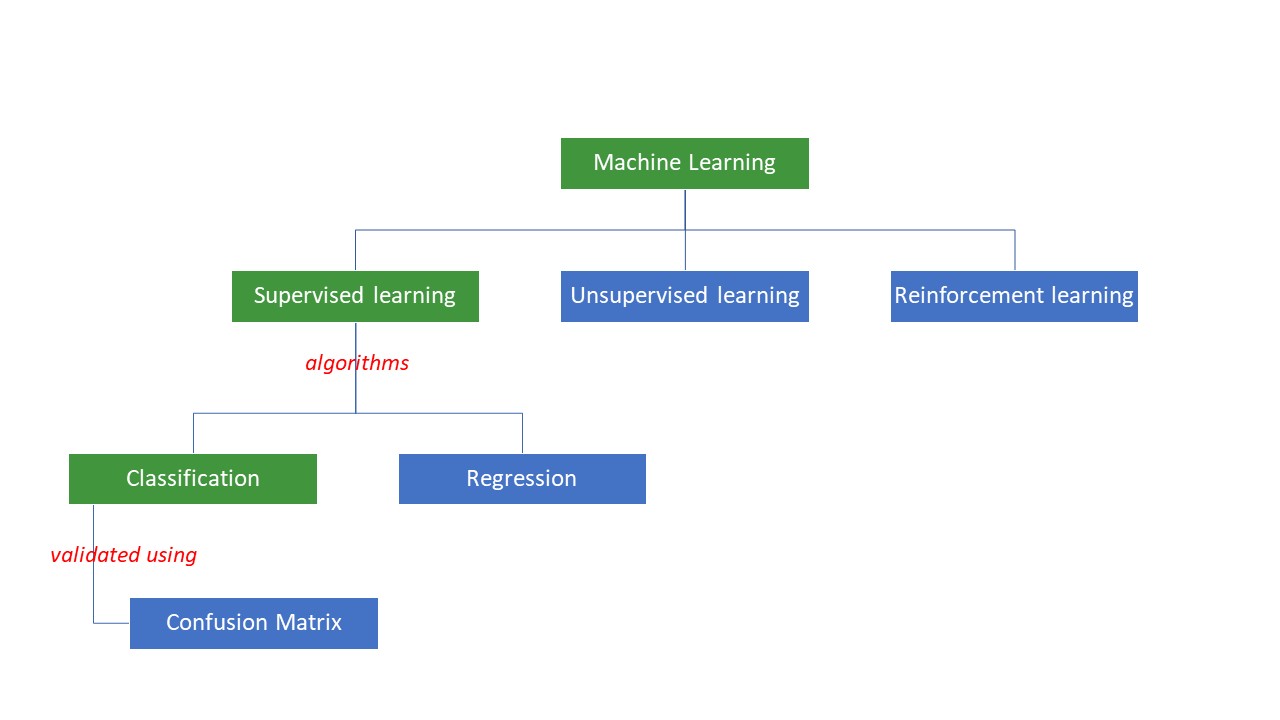
Los tipos más sencillos de algoritmos son los supervisados, en los que ya conocemos la respuesta y entrenamos a las máquinas para que lleguen a esa respuesta entrenando al algoritmo con muchos datos, de la misma forma que un niño diferenciaría entre personas de distintos grupos de edad observando sus rasgos una y otra vez.

Los algoritmos de ML supervisado son de dos tipos: clasificación y regresión.

Los algoritmos de clasificación clasifican u ordenan los datos basándose en algún conjunto de criterios. Por ejemplo, si quiere que su algoritmo agrupe a los clientes en función de sus preferencias alimentarias -a los que les gusta la pizza y a los que no-, utilizaría un algoritmo de clasificación como árbol de decisión, bosque aleatorio, Bayes ingenuo o SVM(Support Vector Machine).

¿Cuál de estos algoritmos haría el mejor trabajo? ¿Por qué debería elegir un algoritmo en lugar de otro?

Introduzca la matriz de confusión….

Una matriz de confusión es una matriz o tabla que ofrece información sobre la precisión de un algoritmo de clasificación a la hora de clasificar un conjunto de datos. Bueno, el nombre no es para confundir a los humanos, ¡pero demasiadas predicciones incorrectas probablemente significan que el algoritmo se confundió😉!

Así pues, una matriz de confusión es un método para evaluar el rendimiento de un algoritmo de clasificación.

¿Cómo?

Supongamos que aplica diferentes algoritmos a nuestro problema binario mencionado anteriormente: clasificar (segregar) a las personas en función de si les gusta o no la pizza. Para evaluar el algoritmo que tiene los valores más cercanos a la respuesta correcta, utilizaría una matriz de confusión. Para un problema de clasificación binaria (me gusta/no me gusta, verdadero/falso, 1/0), la matriz de confusión da cuatro valores de cuadrícula, a saber

• Verdadero Positivo (TP)
• Verdadero Negativo (TN)
• Falso Positivo (FP)
• Falso Negativo (FN)

¿Cuáles son las cuatro cuadrículas de una matriz de confusión?

Los cuatro valores determinados mediante la matriz de confusión forman las rejillas de la matriz.

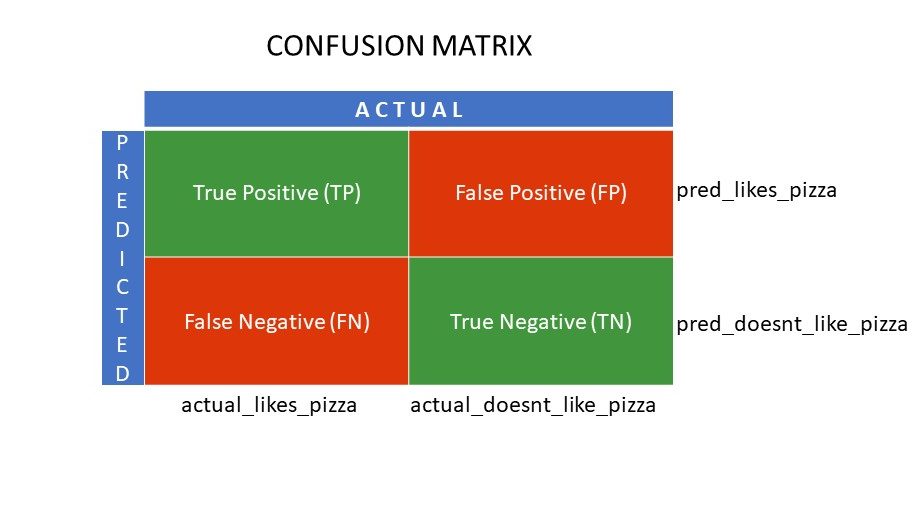
Verdadero Positivo (TP) y Verdadero Negativo (TN) son los valores predichos correctamente por el algoritmo de clasificación,

• TP representa a aquellos a los que les gusta la pizza y el modelo los clasificó correctamente,
• TN representa a los que no les gusta la pizza, y el modelo los clasificó correctamente,

Los falsos positivos (FP) y los falsos negativos (FN) son los valores predichos erróneamente por el clasificador,

• FP representa a aquellos a los que no les gusta la pizza (negativo), pero el clasificador predijo que les gustaba la pizza (erróneamente positivo). FP también se denomina error de tipo I.
• FN representa a aquellos a los que les gusta la pizza (positivo), pero el clasificador predijo que no les gusta (erróneamente negativo). FN también se denomina error de tipo II.

Para entender mejor el concepto, tomemos un escenario de la vida real.

Supongamos que tiene un conjunto de datos de 400 personas que se sometieron a la prueba Covid. Ahora, tiene los resultados de varios algoritmos que determinaron el número de personas Covid positivas y Covid negativas.

Aquí tiene las dos matrices de confusión para compararlas:

Al observar ambas, podría tener la tentación de decir que el^1er algoritmo es más preciso. Pero, para obtener un resultado concreto, necesitamos algunas métricas que puedan medir la exactitud, la precisión y muchos otros valores que demuestren qué algoritmo es mejor.

Métricas que utilizan la matriz de confusión y su significado

Las principales métricas que nos ayudan a decidir si el clasificador hizo las predicciones correctas son:

#1. Recall/Sensibilidad

Recall o Sensibilidad o Tasa de Verdaderos Positivos (TPR) o Probabilidad de Detección es la relación entre las predicciones positivas correctas (TP) y el total de positivas (es decir, TP y FN).

R = TP/(TP FN)

Recall es la medida de resultados positivos correctos devueltos sobre el número de resultados positivos correctos que podrían haberse producido. Un valor más alto de Recall significa que hay menos falsos negativos, lo que es bueno para el algoritmo. Utilice Recall cuando conocer los falsos negativos sea importante. Por ejemplo, si una persona tiene múltiples obstrucciones en el corazón y el modelo muestra que está absolutamente bien, podría resultar fatal.

#2. Precisión

La precisión es la medida de los resultados positivos correctos de entre todos los resultados positivos pronosticados, incluyendo tanto los verdaderos como los falsos positivos.

Pr = TP/(TP FP)

La precisión es muy importante cuando los falsos positivos son demasiado importantes para ser ignorados. Por ejemplo, si una persona no tiene diabetes, pero el modelo así lo indica, y el médico le receta determinados medicamentos. Esto puede provocar graves efectos secundarios.

#3. Especificidad

La especificidad o tasa de verdaderos negativos (TNR) son los resultados negativos correctos encontrados de entre todos los resultados que podrían haber sido negativos.

S = TN/(TN FP)

Es una medida de lo bien que su clasificador está identificando los valores negativos.

#4. Precisión

La exactitud es el número de predicciones correctas sobre el número total de predicciones. Así, si ha encontrado correctamente 20 valores positivos y 10 negativos de una muestra de 50, la exactitud de su modelo será de 30/50.

Precisión A = (TP TN)/(TP TN FP FN)

#5. Prevalencia

La prevalencia es la medida del número de resultados positivos obtenidos de entre todos los resultados.

P = (TP FN)/(TP TN FP FN)

#6. Puntuación F

A veces, es difícil comparar dos clasificadores (modelos) utilizando sólo Precisión y Recall, que no son más que medias aritméticas de una combinación de las cuatro cuadrículas. En tales casos, podemos utilizar la Puntuación F o Puntuación F1, que es la media armónica, más precisa porque no varía demasiado para valores extremadamente altos. Una puntuación F más alta (máximo 1) indica un modelo mejor.

Puntuación F = 2*Precisión*Recall/ (Recall Precision)

Cuando es vital tener en cuenta tanto los falsos positivos como los falsos negativos, la puntuación F1 es una buena métrica. Por ejemplo, no es necesario aislar innecesariamente a los que no son Covid positivos (pero el algoritmo así lo demostró). Del mismo modo, los que son Covid positivos (pero el algoritmo dijo que no lo eran) necesitan ser aislados.

#7. Curvas ROC

Parámetros como la Exactitud y la Precisión son buenas métricas si los datos están equilibrados. Para un conjunto de datos desequilibrado, una precisión alta no significa necesariamente que el clasificador sea eficiente. Por ejemplo, 90 de cada 100 estudiantes de un lote saben español. Ahora bien, aunque su algoritmo diga que los 100 saben español, su precisión será del 90%, lo que puede dar una imagen errónea sobre el modelo. En casos de conjuntos de datos desequilibrados, las métricas como la ROC son determinantes más eficaces.

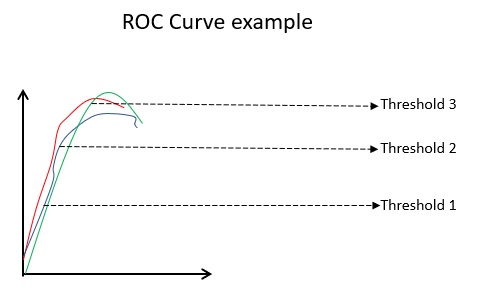
La curva ROC(Receiver Operating Characteristic) muestra visualmente el rendimiento de un modelo de clasificación binaria en varios umbrales de clasificación. Es un gráfico de TPR (Tasa de verdaderos positivos) frente a FPR (Tasa de falsos positivos), que se calcula como (1-Especificidad) en diferentes valores de umbral. El valor más cercano a 45 grados (arriba a la izquierda) en el gráfico es el valor de umbral más preciso. Si el umbral es demasiado alto, no tendremos muchos falsos positivos, pero obtendremos más falsos negativos y viceversa.

Generalmente, cuando se traza la curva ROC de varios modelos, el que tiene la mayor Área Bajo la Curva (AUC) se considera el mejor modelo.

Calculemos todos los valores métricos para nuestras matrices de confusión de los clasificadores I y II:

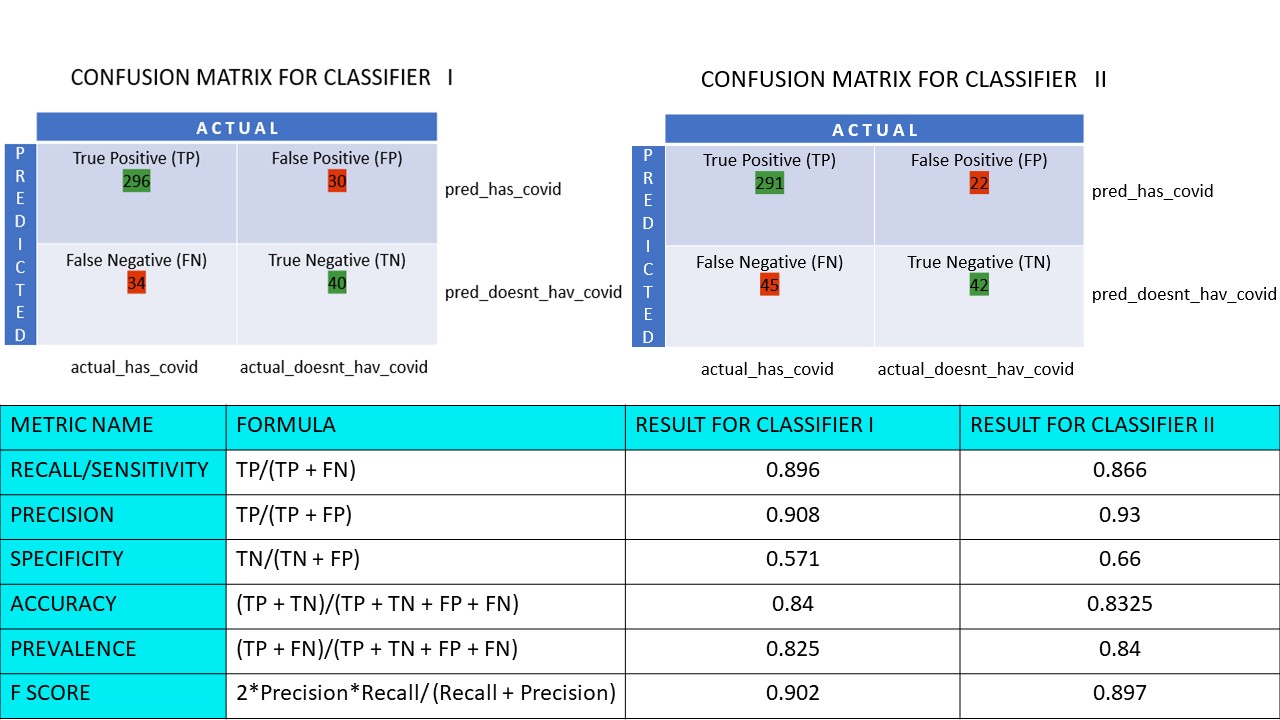
Vemos que la precisión es mayor en el clasificador II, mientras que la exactitud es ligeramente superior en el clasificador I. En función del problema planteado, los responsables de la toma de decisiones pueden seleccionar los clasificadores I o II.

Matriz de confusión N x N

Hasta ahora, hemos visto una matriz de confusión para clasificadores binarios. ¿Qué pasaría si hubiera más categorías que sólo sí/no o me gusta/no me gusta? Por ejemplo, si su algoritmo tuviera que clasificar imágenes de colores rojo, verde y azul. Este tipo de clasificación se denomina clasificación multiclase. El número de variables de salida también decide el tamaño de la matriz. Así, en este caso, la matriz de confusión será de 3×3.

Resumen

Una matriz de confusión es un gran sistema de evaluación, ya que proporciona información detallada sobre el rendimiento de un algoritmo de clasificación. Funciona bien tanto para los clasificadores binarios como para los multiclase, en los que hay que tener en cuenta más de 2 parámetros. Es fácil visualizar una matriz de confusión, y podemos generar todas las demás métricas de rendimiento como la puntuación F, la precisión, el ROC y la exactitud utilizando la matriz de confusión.

También puede ver cómo elegir algoritmos ML para problemas de regresión.