Cómo realizar la división en planta en Python

En este tutorial, aprenderá a realizar la división por el suelo en Python. Utilizará el operador // de Python, la función floor del módulo math de Python, y más – con ejemplos de código.

Comenzaremos con una visión general de los operadores aritméticos en Python y aprenderemos cómo funciona el operador de división por el suelo //. A continuación, aprenderemos a utilizar otros métodos equivalentes, incluidas las funciones de los módulos math y operator para realizar la división por el suelo.

Empecemos…

Operadores aritméticos en Python

En Python, puede utilizar operadores aritméticos para realizar operaciones aritméticas sencillas sobre números de los tipos de datos int y float. Estos operadores actúan sobre los operandos (los números) y devuelven el resultado de la operación.

La siguiente tabla resume los operadores aritméticos en Python y cómo funcionan:

Operador	Sintaxis	Resultado
Suma ( )	`num1 num2`	Devuelve la suma de `num1` y `num2`
Sustracción (-)	`num1-num2`	Devuelve la diferencia entre `num1` y `num2`
Multiplicación (*)	`num1*num2`	Devuelve el producto de `num1` y `num2`
Exponenciación (**)	`num1**num2`	Devuelve el resultado de `num1` elevado a la potencia de `num2`; ^num1num2
División (/)	`num1/num2`	Devuelve el resultado de dividir `num1` por `num2` – incluyendo la parte fraccionaria
División por el suelo (/)	`num1//num2`	Devuelve el cociente cuando `num1` se divide por `num2`
Módulo (%)	`num1 % num2`	Devuelve el resto cuando `num1` se divide por `num2`

Veamos algunos ejemplos que utilizan estos operadores aritméticos. Puede probar estos ejemplos en un REPL de Python o en el editor de Python en línea de Geekflare.

>>> num1 = 18
>>> num2 = 5

>>> num1 num2
23

>>> num1 - num2
13

>>> num1 * num2
90

>>> num1 ** num2
1889568

En este ejemplo, num1 es 18 y num2 es 5. La operación de división num1/num2 devuelve el resultado incluyendo la parte fraccionaria.

El número 5 entra tres veces en 18 dejando un resto de tres. Por lo tanto, la operación de división por el suelo, num1//num2, da el cociente 3, mientras que el operador de módulo da el resto, también 3 en este caso.

>>> num1/num2
3.6

>>> num1//num2
3

>>> num1 % num2
3

Esto debería darle una idea de cómo funcionan los operadores de división, división piso y módulo. A continuación, aprenderemos sobre el operador de división piso en detalle.

⚠️ En Python 2, la operación de división (/) trunca el resultado al número entero más cercano, de forma similar a la operación de división por el suelo en Python 3. Este tutorial analiza cómo funciona la operación de división por el suelo en Python 3.x.

División por el suelo con el operador //

Considere una operación de división con un dividendo y un divisor. En num1/num2, num1 es el dividendo y num2 es el divisor. Para realizar la división por el suelo de num1 y num2, utilice num1//num2.

El operador de división por el suelo (//) devuelve el cociente de la operación de división-como un número entero o de coma flotante-dependiendo de los tipos de datos de los operandos.

El operador de división por el suelo no garantiza que la respuesta sea siempre un número entero. Si el dividendo(num1) o el divisor(num2) es un flotante, entonces el resultado de num1//num2 es un flotante. He aquí algunos ejemplos.

>>> 18.0//5
3.0
>>> 10.0//4
2.0
>>> 15//4.0
3.0

Si necesita que el resultado sea un número entero, deberá convertirlo explícitamente en un número entero utilizando la función int():

>>> int(18.0//5)
3
>>> int(10.0//4)
2
>>> int(15//4.0)
3

¿Qué ocurre bajo el capó?

Cuando utiliza el operador de división piso //, se llama al método especial (también llamado método dunder) __floordiv__ (). Por lo tanto, también puede utilizar el método __floordiv__ () en cualquier número entero o de coma flotante, como se muestra a continuación:

num1 = 18
num2 = 5
num1.__floordiv__(num2)
# Salida 3

División por el suelo utilizando operator.floordiv()

💡 Para realizar la división por el suelo en Python, también puede utilizar la función floordiv() del módulo operador.

El módulo operador de Python contiene las definiciones de funciones eficientes que pueden realizar todas las operaciones aritméticas. Por lo tanto, para realizar la división por el suelo, también puede utilizar la función floordiv () del módulo operador – en lugar del operador //.

Utilizar la función floordiv () del módulo operador equivale a utilizar el operador de división por el suelo.

>>> importar operador
>>> operator.floordiv(18,5)
# Salida 3
>>> operator.floordiv(12,5.0)
# Salida 2.0

División por el suelo utilizando math.floor()

¿Cómo funciona la función floor?

En matemáticas, la función floor( ) toma cualquier número real x como entrada y devuelve un número entero (resultado). Este resultado es el mayor número entero que es menor o igual que el número real x.

Para entenderlo mejor, tomemos algunos ejemplos y visualicemos estos números en una recta numérica.

Ejemplo 1: Consideremos el número 2,3. El mayor número entero que es menor o igual que 2,3 es 2; por lo que floor(2,3) devolverá 2.

Ejemplo 2: También puede aplicar la misma definición cuando trabaje con números negativos. Considere el número -1,7. El mayor número entero que es menor o igual que -1,7 es -2; por lo que floor(-1,7) devolverá -2.

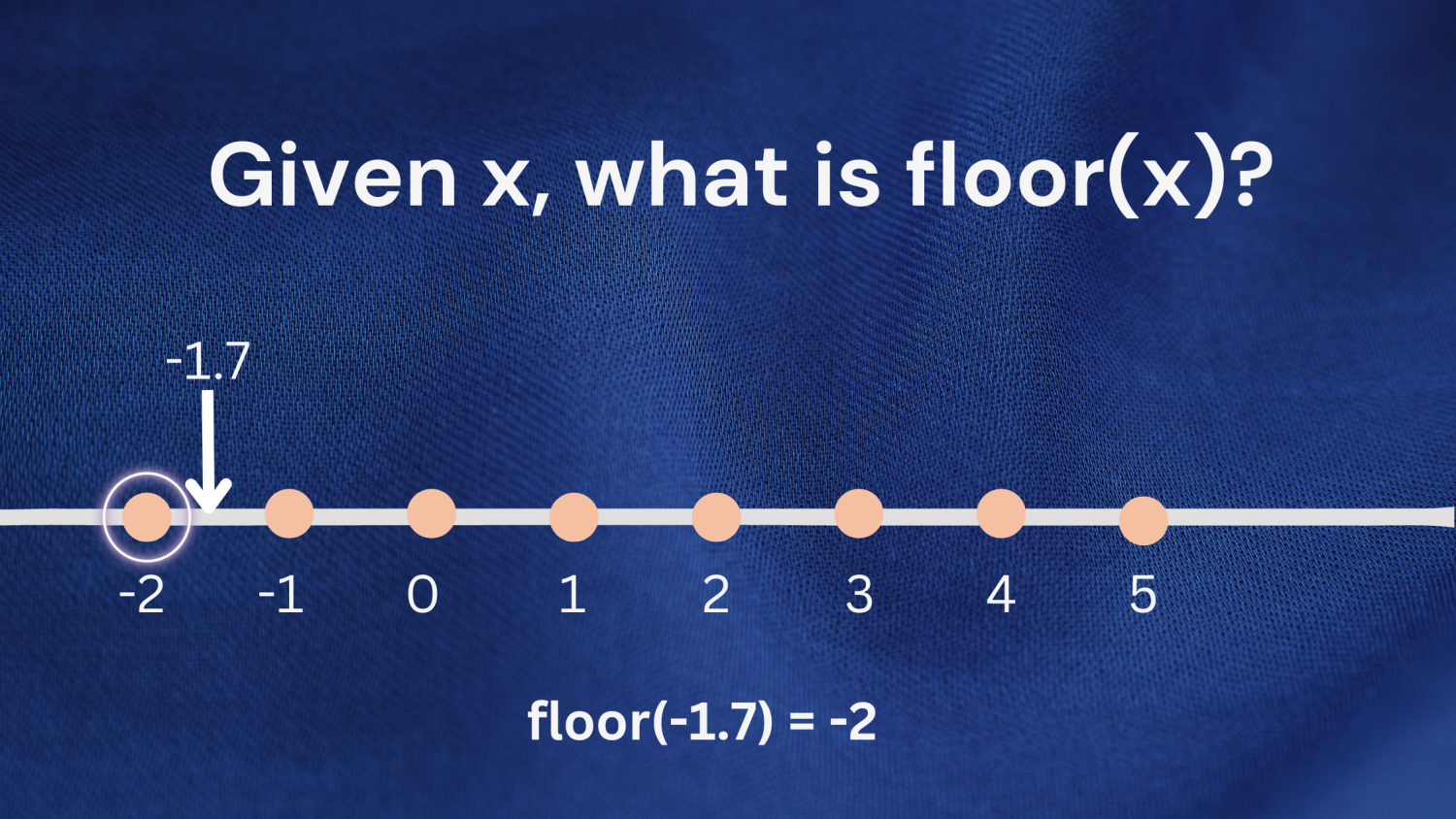
Verifiquemos los resultados anteriores utilizando la función floor() del módulo math.

>>> from math import floor
>>> floor(2.3)
2
>>> floor(-1.7)
-2

Para realizar la división por el suelo, puede llamar a la función floor() con num1/num2 como argumento. Como trunca o redondea el resultado al entero más cercano, es equivalente a la operación de división por el suelo.

Puede importar explícitamente la función floor( ) del módulo math, como se muestra:

from math import suelo
num1 = 18
num2 = 5
floor(num1/num2)
# Salida 3

Alternativamente, también puede importar sólo el módulo math y luego acceder a la función floor( ) utilizando math.floor().

importar math
num1 = 18
num2 = 5
math.floor(num1/num2)
# Salida 3

A diferencia de la función floordiv() del módulo de operadores y del operador de división piso //, el uso de math .floor(num1/num2) garantiza que el resultado es un número entero. Este método hace que el código sea legible y elimina el paso de fundición de tipos.

importar math
num1 = 18.0
num2 = 5
math.floor(num1/num2)
# Salida 3

Ejemplos de división por el suelo en Python

Concluyamos nuestra discusión con un ejemplo práctico: Búsqueda binaria. ✅

📑 La búsqueda binaria es un algoritmo de búsqueda eficiente que le permite buscar un elemento objetivo a través de matrices ordenadas en tiempo O(log n), donde n es el tamaño de la matriz.

Este algoritmo funciona dividiendo el intervalo de búsqueda por la mitad en cada paso. Esto se hace dependiendo de si el punto medio del intervalo coincide con el objetivo (¡la búsqueda termina cuando se encuentra la coincidencia!) o es menor o mayor que el objetivo. Como el tamaño de la matriz se reduce a la mitad en cada paso, el punto medio no siempre se evalúa como un número entero.

itemlist = [5,7,18,21,34,45]
item = 7

Considere la siguiente implementación del algoritmo de búsqueda binaria. La función binary_search() toma un número(item) y una lista(itemlist) y busca la ocurrencia del item en itemlist.

Si se encuentra el elemento, la función devuelve el índice en el que aparece el elemento.
Si no, devuelve Ninguno.

def binary_search(item, itemlist):
    # obtener el tamaño de la lista
    tamaño_lista = len(itemlist) - 1
    # empezar en los dos extremos de la lista
    lowerIdx = 0
    upperIdx = listsize
    while lowerIdx <= upperIdx:
        # calcule el punto medio
        # utilice la división normal en lugar de la división por pisos
        midPt = (lowerIdx upperIdx)/ 2 
        # si se encuentra el punto, devuelva el índice
        if itemlist[midPt] == item:
            return midPt
        # de lo contrario obtenga el siguiente punto medio
        si item > itemlist[midPt]:
            lowerIdx = midPt 1
        si no
            upperIdx = midPt - 1
    si lowerIdx > upperIdx
        return None

Esta implementación es funcionalmente correcta excepto porque no hemos tenido en cuenta que midPt no se evalúa a un entero a medida que avanza la búsqueda.

binary_search(item,itemlist)

Si llamamos a la función, nos encontramos con un TypeError que indica que los índices de la lista deben ser enteros o trozos, no flotantes.

---------------------------------------------------------------------------
TypeError Traceback (most recent call last)
 en 
 1 binary_search(item,itemlist)
 en binary_search(item, itemlist)
     12 
     13 # si se encuentra item, devuelve el índice
--->
 14 if itemlist[midPt] == item:
     15 return midPt
     16 # de lo contrario obtiene el siguiente punto medio
TypeError: los índices de la lista deben ser enteros o cortes, no flotantes

Modificamos la definición de la función para utilizar el operador de división piso:

def binary_search(item, itemlist):
    # obtener el tamaño de la lista
    tamaño_lista = len(itemlist) - 1
    # empezar en los dos extremos de la lista
    lowerIdx = 0
    upperIdx = listsize
    while lowerIdx <= upperIdx:
        # calcule el punto medio
        # utilice la división por pisos
        midPt = (lowerIdx upperIdx)// 2 
        # si se encuentra el elemento, devuelva el índice
        if itemlist[midPt] == item:
            return midPt
        # en caso contrario obtenga el siguiente punto medio
        si item > itemlist[midPt]:
            lowerIdx = midPt 1
        si no
            upperIdx = midPt - 1
    si lowerIdx > upperIdx
        return None

La función devuelve el índice en el que se encuentra el elemento 7, que es el índice uno.

binary_search(item,itemlist)
# Salida 1

Conclusion

Espero que este tutorial le haya ayudado a entender cómo realizar la división por el suelo en Python. Aquí tiene un resumen de los diferentes métodos que ha aprendido:

En Python, un operador b realiza la operación definida por el operador con a y b como operandos y devuelve el resultado de la operación.
Puede utilizar el operador de división por el suelo de Python //; a//b devuelve el cociente de la operación de división a/b.
Alternativamente, puede utilizar la función equivalente floordiv() definida en el módulo operador de Python con la sintaxis: operador.floordiv(a,b) para obtener el resultado de a//b.
Todos los métodos anteriores devuelven el cociente, pero el tipo de datos puede ser un float o un int dependiendo de los valores de a y b. Así que tendrá que convertir el valor de retorno a un entero.
La función floor() del módulo math de Python también puede utilizarse para realizar la división por el suelo: math.floor(a,b) es equivalente a a//b y devuelve un entero. Cuando desee que el resultado sea un entero, considere utilizar la función floor del módulo math.

Bala Priya C
Colaborador
Bala Priya es una desarrolladora y redactora técnica india con más de tres años de experiencia en la redacción de contenidos técnicos. Comparte sus conocimientos con la comunidad de desarrolladores escribiendo tutoriales técnicos, guías prácticas y mucho más. Actualmente trabaja como editora técnica en Geekflare. También colabora activamente en otras publicaciones técnicas como freeCodeCamp y KDnuggets.