Explicado: Qué es la modelización multinivel [+3 Recursos de aprendizaje]

Esta completa guía incluye todo lo que usted, como principiante, necesita saber sobre el modelado multinivel, una técnica utilizada para tratar datos agrupados o en conglomerados.

El modelado multinivel, también conocido como modelado lineal jerárquico, modelos mixtos y modelado de efectos aleatorios, se utiliza en distintos ámbitos como la investigación médica, la economía, la sociología, el marketing, la psicología educativa y otros campos.

El modelado multinivel también se utiliza en el sector del marketing para el análisis avanzado de encuestas, el modelado de la respuesta del mercado y la gestión de las relaciones con los clientes.

Modelización multinivel

El modelado multinivel es una técnica para gestionar datos de forma agrupada o clusterizada. Este procedimiento también puede utilizarse para analizar los datos con medidas repetidas. El término multinivel indica datos jerárquicos o anidados, y análisis multinivel significa estudiar las relaciones entre variables medidas en distintos niveles de la estructura de datos multinivel.

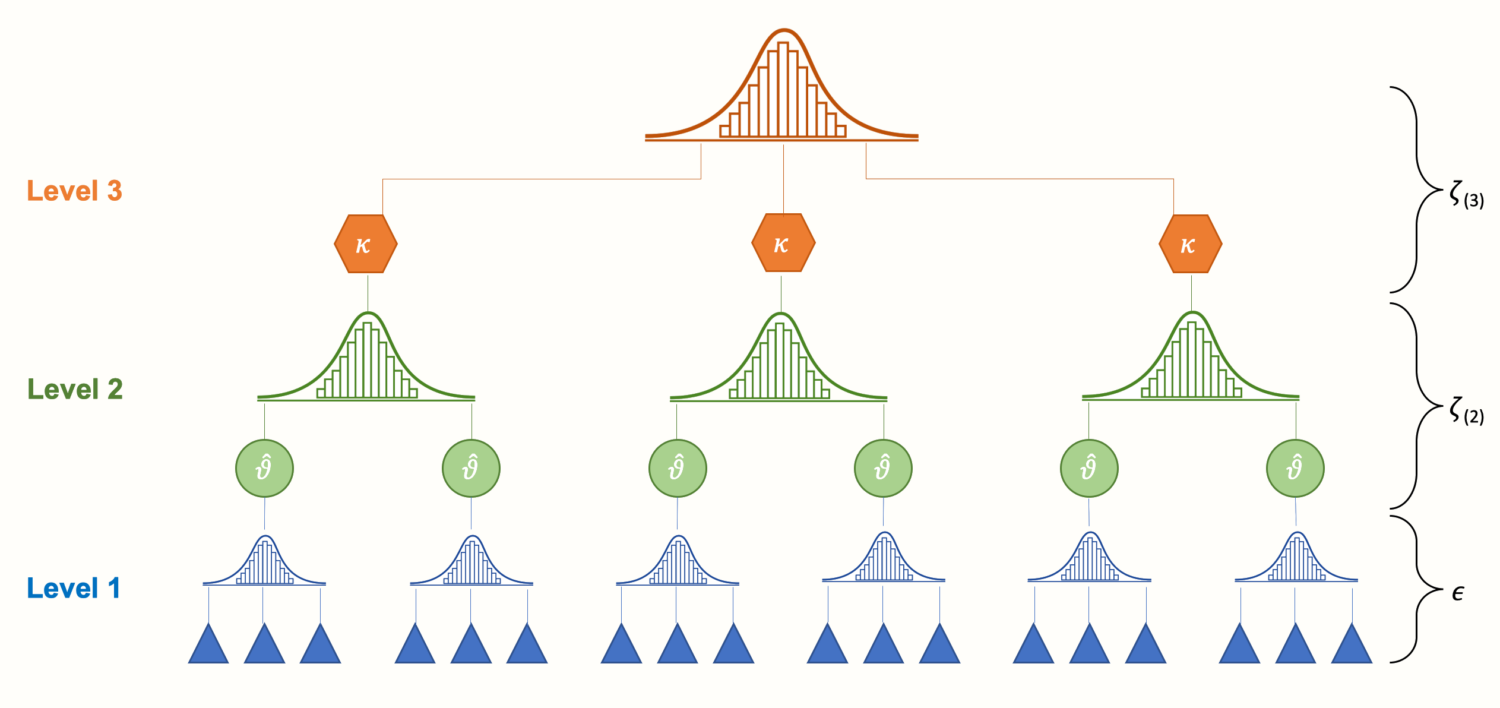
Consideremos un escenario. Supongamos que a una enfermera se le ha asignado la tarea de registrar la tensión arterial de un grupo de pacientes cada semana. Pueden considerar las mediciones sucesivas como un grupo dentro de cada sujeto.

En definitiva, el modelado multinivel puede manejar datos con diferentes periodos de medición de un sujeto a otro. En aprendizaje automáticoel modelo multinivel puede emplearse en escenarios que contienen parámetros que varían en varios niveles.

Profundicemos en los conceptos del modelado multinivel.

Ventajas de la modelización multinivel

El enfoque de modelización multinivel para modelizar la variación entre grupos ofrece varias ventajas.

Hacer mejores inferencias

El modelo de regresión normal no tiene en cuenta la población más amplia, lo que provoca una subestimación de los coeficientes y una sobrestimación de la significación de los mismos. En cambio, la modelización multinivel permite hacer mejores inferencias sobre la curva de crecimiento de los datos agrupados de los que se ha extraído la muestra.

Se necesitan menos parámetros

Un modelo de regresión normal requiere varias variables ficticias para representar un grupo de datos complejo. En cambio, el modelado multinivel necesita menos perímetros para lo mismo.

Efectos de grupo

Los modelos multinivel permiten compartir información entre grupos al suponer que los efectos aleatorios proceden de una distribución común. Esto, a diferencia de la regresión normal, mejora enormemente la precisión de la predicción para los grupos con menos datos.

Tipos de modelos multinivel

Pasemos ahora a analizar los distintos tipos de modelos multinivel.

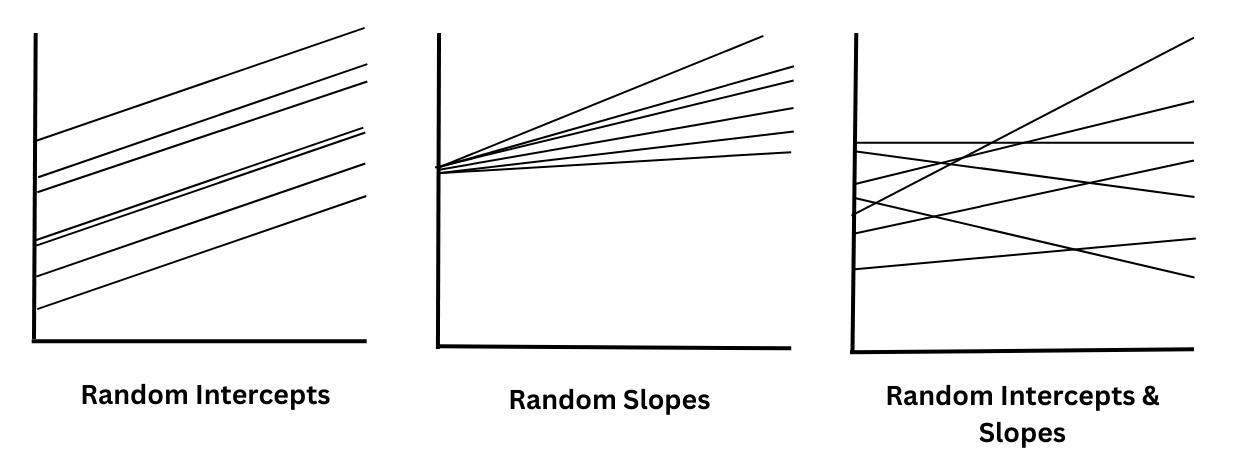
#1. Modelo de interceptos aleatorios

En el Modelo de Interceptos Aleatorios, el término de intercepción puede variar en el conglomerado. Es necesario añadir una variable aleatoria para representar el término de intercepción que ayuda a predecir las puntuaciones en la variable dependiente para cada observación.

Este modelo supone que las pendientes permanecen constantes en los distintos contextos y proporciona información sobre las correlaciones intraclase, que desempeña un papel fundamental a la hora de determinar si realmente es necesario aplicar el modelo multinivel o no.

#2. Modelo de pendientes aleatorias

En el modelo de pendientes aleatorias, las pendientes fluctúan con respecto a la matriz de correlaciones y, por lo tanto, las pendientes tienden a diferir según las variables de agrupación, como el tiempo o los individuos.

También en este caso, los interceptos permanecen fijos en los distintos contextos. El modelo de pendiente aleatoria o modelo de coeficiente ayuda a comprender la variabilidad entre los grupos, que no es posible determinar únicamente mediante el modelo de intercepto aleatorio.

#3. Modelo de interceptos y pendientes aleatorios

En este modelo, como su nombre indica, tanto los interceptos como las pendientes pueden variar entre los grupos. Esto significa que su valor cambia en diferentes contextos. El modelo de interceptos y pendientes aleatorios se considera el tipo de modelo más realista.

¿Cómo funciona la modelización multinivel?

Los modelos multinivel son un tipo de modelo estadístico que considera múltiples niveles de variación. Estos modelos también se conocen como modelos lineales jerárquicos, modelos lineales de efectos mixtos, modelos mixtos, anidados modelos de datosLos modelos de efectos aleatorios, los modelos de parámetros aleatorios o los diseños de parcelas divididas.

Diferentes tipos de datos recogidos a partir de observaciones realizadas durante la investigación humana y las ciencias biológicas muestran una estructura jerárquica o agrupada.

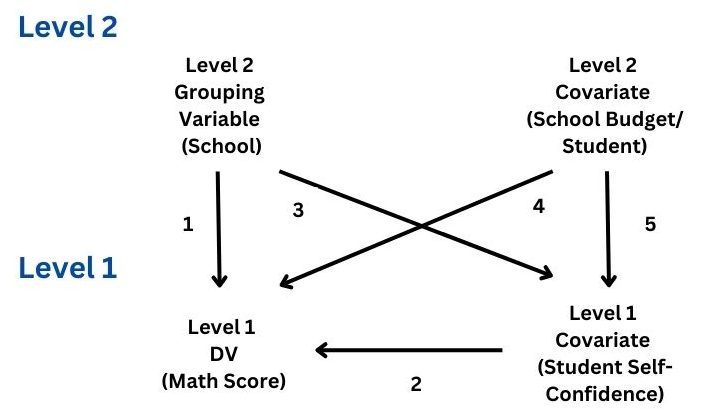
Por ejemplo, los niños que tienen los mismos padres biológicos poseen características físicas y mentales similares en mayor medida que los individuos elegidos al azar de una población más amplia.

Del mismo modo, los empleados o estudiantes pueden segregarse en función de factores individuales como la ubicación. Las acciones individuales vinculadas progresivamente también dan lugar a estructuras de datos multinivel.

Los modelos multinivel consideran elementos residuales en cada nivel dentro de la estructura jerárquica para dar lugar a la formación de una estructura de datos jerárquica.

Los modelos estratificados también ayudan a las autoridades escolares a organizar los resultados de los alumnos, que suelen incluir los residuales tanto a nivel de centro como de alumno.

Para los no iniciados, los residuos escolares, o efectos relacionados con la escuela, son un conjunto de características escolares no observadas que pueden influir en los resultados de los alumnos. Estos efectos pueden desencadenar la relación entre los resultados de los alumnos. De ahí que resulte seguro dividir la varianza de los residuos en dos partes: un componente entre escuelas y un componente dentro de la escuela.

¿Cuándo se debe utilizar la modelización multinivel?

He aquí algunas razones por las que debería preferir utilizar modelos multinivel:

Hacer inferencias correctas

En los métodos estándar de regresión múltiple, la unidad de análisis se considera una observación independiente.

La incompetencia de la regresión múltiple para reconocer las estructuras jerárquicas provoca una subestimación de los errores normales, lo que lleva a una sobreestimación de la significación estadística. La omisión de la agrupación afecta en gran medida a la precisión de las predicciones para las variables predictoras de alto nivel.

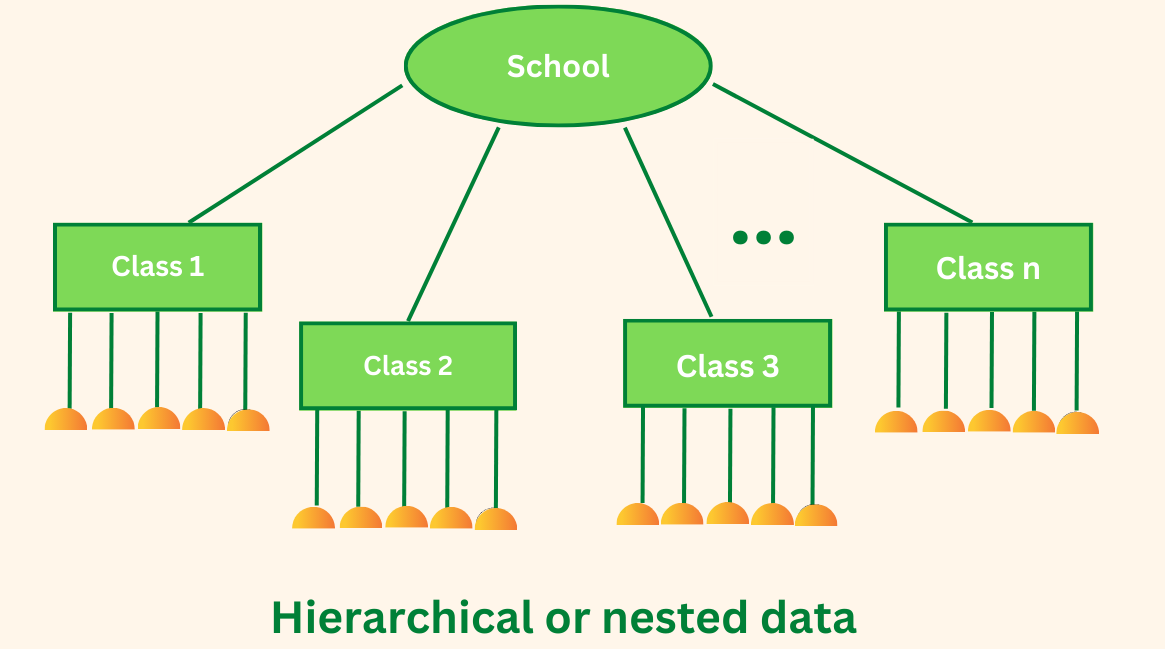
Inferencia a una población de grupos

El modelo multinivel trata los grupos de la muestra como una muestra aleatoria escogida de un grupo, lo que constituye un importante ámbito de investigación en varios casos. Esto no puede lograrse con el modelo de efectos fijos, en el que es imposible hacer inferencias más allá de los grupos de la muestra.

Evaluación de los efectos de grupo

La modelización multinivel es el mejor método para determinar los efectos separados sobre las observaciones y las características no observadas del grupo.

Interés sustancial en los efectos de grupo

En varios ámbitos de investigación, una cuestión clave se refiere al alcance de la agrupación en los resultados individuales y a la determinación de su existencia en los grupos "periféricos".

Por ejemplo, en las evaluaciones del rendimiento escolar, el objetivo clave es identificar los efectos de "valor añadido" relacionados con la escuela sobre el rendimiento de los alumnos. Esto puede determinarse mediante un modelo multinivel tras ajustar los logros previos.

Recursos de aprendizaje

Estos son los mejores materiales didácticos que puede consultar para comprender los conceptos del modelado multinivel.

#1. Modelización multinivel en lenguaje sencillo

Multilevel Modeling in Plain Language, de Karen Robson y David Pavalin, es uno de los mejores libros sobre modelización multinivel, ya que presenta las fases completas de un análisis multinivel tanto para estudiantes como para instructores.

Vista previa	Producto	Valoración	Precio
	Modelización multinivel en lenguaje sencillo	No hay valoraciones	$32.51	Comprar en Amazon

El "enfoque llano" del libro ayuda al lector a captar la idea que subyace al tema en lugar de explicar la fórmula que se encuentra en otros materiales didácticos. Del mismo modo, los educadores podrán ponerse al día muy rápidamente en el camino avanzado del análisis multinivel.

#2. Análisis Multinivel: Una introducción a la modelización multinivel

Escrito por T. A. B. Snijders, Multilevel Analysis: An Introduction To Basic And Advanced Multilevel Modeling ofrece un contenido accesible sobre el análisis multinivel adaptado para satisfacer las necesidades de investigadores avanzados y profesores que deseen realizar investigaciones en el mismo campo.

Vista previa	Producto	Valoración	Precio
	Análisis Multinivel: Una introducción a la modelización multinivel básica y avanzada	No hay valoraciones	$44.49	Comprar en Amazon

Aparte de eso, los lectores que deseen ampliar sus conocimientos en el campo del análisis multinivel encontrarán en este libro un recurso ideal.

El libro abarca los distintos métodos, técnicas y cuestiones que giran en torno a la modelización y el análisis multinivel y proporciona a los lectores una comprensión clara, conceptual y práctica de los estudios multinivel.

#3. Modelización multinivel con R

Multilevel Modeling Using R de W. Holmes Finch, Jocelyn E. Bolin y Ken Kelley es una valiosa guía sobre la modelización de datos multinivel utilizando el entorno de software R. El libro revisa y presenta los fundamentos de los modelos multinivel y explica cómo implementar estos modelos utilizando R.

Vista previa	Producto	Valoración	Precio
	Modelización multinivel con R (Chapman & Hall/CRC Statistics in the Social and Behavioral Sciences)		$46.34	Comprar en Amazon

También demuestra el proceso de emplear modelos multinivel con datos longitudinales. Aparte de esto, también encontrará los modelos para variables dependientes categóricas tanto en datos de un solo nivel como multinivel.

Conclusión

Aquí hemos tratado los conceptos básicos del modelado multinivel, desde sus ventajas hasta cómo funciona la técnica. Si es usted estudiante o educador, el material didáctico mencionado le ofrecerá una valiosa ayuda para comprender los conceptos avanzados del modelado multinivel.

También puede explorar algunos modelos de aprendizaje automático.