3 formas de multiplicar matrices en Python

En este tutorial, aprenderá a multiplicar dos mat rices en Python.

Comenzará aprendiendo la condición para una multiplicación matricial válida y escribirá una función personalizada de Python para multiplicar matrices. A continuación, verá cómo puede conseguir el mismo resultado utilizando comprensiones de listas anidadas.

Por último, procederá a utilizar NumPy y sus funciones incorporadas para realizar la multiplicación de matrices de forma más eficiente.

Cómo comprobar si la multiplicación matricial es válida

Antes de escribir código Python para la multiplicación de matrices, repasemos los conceptos básicos de la multiplicación de matrices.

La multiplicación matricial entre dos matrices A y B sólo es válida si el número de columnas de la matriz A es igual al número de filas de la matriz B.

Es probable que se haya encontrado alguna vez con esta condición para la multiplicación de matrices. Sin embargo, ¿se ha preguntado alguna vez por qué es así?

Pues bien, se debe a la forma en que funciona la multiplicación de matrices. Eche un vistazo a la siguiente imagen.

En nuestro ejemplo genérico, la matriz A tiene m filas y n columnas. Y la matriz B tiene n filas y p columnas.

¿Cuál es la forma de la matriz producto?

El elemento en el índice (i, j) de la matriz resultante C es el producto escalar de la fila i de la matriz A y la columna j de la matriz B.

Así que para obtener un elemento en un índice concreto de la matriz resultante C, tendrá que calcular el producto escalar de la fila y la columna correspondientes en las matrices A y B, respectivamente.

Repitiendo el proceso anterior, obtendrá la matriz producto C de forma m x p-con m filas y p columnas, como se muestra a continuación.

Y el producto punto o producto interior entre dos vectores a y b viene dado por la siguiente ecuación.

Resumamos ahora:

• Es evidente que el producto punto se define sólo entre vectores de igual longitud.
• Por tanto, para que el producto punto entre una fila y una columna sea válido -al multiplicar dos matrices- es necesario que ambas tengan el mismo número de elementos.
• En el ejemplo genérico anterior, cada fila de la matriz A tiene n elementos. Y cada columna de la matriz B también tiene n elementos.

Si lo mira con más detenimiento, n es el número de columnas de la matriz A, y también es el número de filas de la matriz B. Y ésta es precisamente la razón por la que necesita que el número de columnas de la matriz A sea igual al número de filas de la matriz B.

Espero que entienda la condición para que la multiplicación de matrices sea válida y cómo obtener cada elemento en la matriz producto.

Procedamos a escribir algo de código Python para multiplicar dos matrices.

Escribir una función personalizada de Python para multiplicar matrices

Como primer paso, escribamos una función personalizada para multiplicar matrices.

Esta función debería hacer lo siguiente

• Aceptar dos matrices, A y B, como entradas.
• Comprobar si la multiplicación de matrices entre A y B es válida.
• Si es válida, multiplicar las dos matrices A y B, y devolver la matriz producto C.
• En caso contrario, devuelve un mensaje de error indicando que las matrices A y B no pueden multiplicarse.

Paso 1: Genere dos matrices de enteros utilizando la función random.randint() de NumPy. También puede declarar matrices como listas anidadas de Python.

importar numpy como np
np.random.seed(27)
A = np.random.randint(1,10,tamaño = (3,3))
B = np.random.randint(1,10,tamaño = (3,2))
print(f "Matriz A:\n {A}\n")
print(f "Matriz B:\n {B}\n")

# Salida
Matriz A
 [[4 9 9]
 [9 1 6]
 [9 2 3]]

Matriz B:
 [[2 2]
 [5 7]
 [4 4]]

Paso 2: Siga adelante y defina la función multiplicar_matriz(A,B). Esta función toma dos matrices A y B como entradas y devuelve la matriz producto C si la multiplicación de matrices es válida.

def multiplicar_matriz(A,B):
  global C
  si A.forma[1] == B.forma[0]:
    C = np.zeros((A.forma[0],B.forma[1]),dtype = int)
    para fila en rango(filas) 
        for col in range(cols):
            for elt in range(len(B)):
              C[fila, col] = A[fila, elt] * B[elt, col]
    return C
  si no
    return "Lo sentimos, no es posible multiplicar A y B"

Análisis sintáctico de la definición de la función

Procedamos a analizar la definición de la función.

Declare C como una variable global: Por defecto, todas las variables dentro de una función Python tienen ámbito local. Y no se puede acceder a ellas desde fuera de la función. Para que la matriz del producto C sea accesible desde fuera, tendremos que declararla como variable global. Sólo tiene que añadir el calificador global antes del nombre de la variable.

Compruebe si la multiplicación de matrices es válida: Utilice el atributo shape para comprobar si A y B pueden multiplicarse. Para cualquier matriz arr, arr.shape[0] y arr.shape[1] dan el número de filas y columnas, respectivamente. Así, si A.shape[1] == B.shape[0 ] se comprueba si la multiplicación de matrices es válida. Sólo si esta condición es Verdadera, se calculará la matriz producto. De lo contrario, la función devuelve un mensaje de error.

Utilice bucles anidados para calcular valores: Para calcular los elementos de la matriz resultante, tenemos que recorrer las filas de la matriz A, y el bucle for exterior se encarga de ello. El bucle for interior nos ayuda a recorrer las columnas de la matriz B. Y el bucle for más interior nos ayuda a acceder a cada elemento de la columna seleccionada.

▶️ Ahora que hemos aprendido cómo funciona la función de Python para multiplicar matrices, llamemos a la función con las matrices A y B que generamos anteriormente.

multiplicar_matriz(A,B)

# Salida
array([ 89, 107],
       [ 47, 49],
       [ 40, 44]])

Como la multiplicación de matrices entre A y B es válida, la función multiply_matrix() devuelve la matriz producto C.

Utilizar la comprensión de listas anidadas de Python para multiplicar matrices

En la sección anterior, escribió una función de Python para multiplicar matrices. Ahora, verá cómo puede utilizar comprensiones de listas anidadas para hacer lo mismo.

Aquí tiene la comprensión de lista anidada para multiplicar matrices.

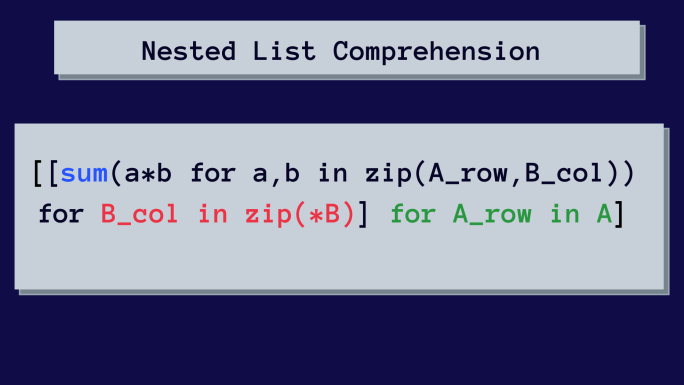
Al principio, esto puede parecer complicado. Pero analizaremos la comprensión de lista anidada paso a paso.

Centrémonos en una comprensión de lista cada vez e identifiquemos lo que hace.

Utilizaremos la siguiente plantilla general para la comprensión de listas:

[ para  en ]

donde
: lo que desea hacer-expresión u operación
: cada elemento sobre el que desea realizar la operación
: el iterable (lista, tupla, etc.) sobre el que está realizando el bucle

▶️ Consulte nuestra guía Comprensión de listas en Python – con ejemplos para obtener una comprensión más profunda.

Antes de seguir adelante, tenga en cuenta que queremos construir la matriz resultante C fila a fila.

Explicación de la comprensión de listas anidadas

Paso 1: Calcular un único valor en la matriz C

Dada la fila i de la matriz A y la columna j de la matriz B, la expresión siguiente da la entrada en el índice (i, j) de la matriz C.

suma(a*b para a,b en zip(fila_A, columna_B)

# zip(A_row, B_col) devuelve un iterador de tuplas
# Si A_row = [a1, a2, a3] & B_col = [b1, b2, b3]
# zip(A_row, B_col) devuelve (a1, b1), (a2, b2), y así sucesivamente

Si i= j = 1, la expresión devolverá la entrada c_11 de la matriz C. Así que puede obtener un elemento en una fila de esta manera.

Paso 2: Construir una fila en la matriz C

Nuestro siguiente objetivo es construir una fila entera.

Para la fila 1 de la matriz A, tiene que recorrer todas las columnas de la matriz B para obtener una fila completa en la matriz C.

Vuelva a la plantilla de comprensión de listas.

• Sustituya por la expresión del paso 1, porque eso es lo que quiere hacer.
• A continuación, sustituya por B_col-cadacolumna de la matriz B.
• Por último, sustituya por zip(*B)-la lista que contiene todas las columnas de la matriz B.

Y he aquí la primera comprensión de la lista.

[suma(a*b para a,b en zip(A_fila, B_col)) para B_col en zip(*B)] 

# zip(*B): * es el operador de descompresión
# zip(*B) devuelve una lista de columnas de la matriz B

Paso 3: Construir todas las filas y obtener la matriz C

A continuación, tendrá que poblar la matriz producto C computando el resto de las filas.

Y para ello, tendrá que recorrer en bucle todas las filas de la matriz A.

Vuelva de nuevo a la comprensión de la lista y haga lo siguiente.

• Sustituya por la comprensión de lista del paso 2. Recuerde que hemos computado una fila entera en el paso anterior.
• Ahora, sustituya por A_row-cadafila de la matriz A.
• Y su es la propia matriz A, ya que está haciendo un bucle a través de sus filas.

Y aquí está nuestra comprensión final de lista anidada.🎊

[[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] 
    for A_row in A]

¡Es hora de verificar el resultado! ✔

# cast into NumPy array using np.array()
C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)] 
    for A_row in A])

# Salida:
[[ 89 107]
 [ 47 49]
 [ 40 44]]

Si echa un vistazo más de cerca, esto es equivalente a los bucles for anidados que teníamos antes, sólo que es más sucinto.

También puede hacer esto de forma aún más eficiente utilizando algunas funciones incorporadas. Vamos a aprender acerca de ellos en la siguiente sección.

Utilice NumPy matmul() para multiplicar matrices en Python

La función np.mat mul() toma dos matrices como entrada y devuelve el producto si la multiplicación matricial entre las matrices de entrada es válida.

C = np.matmul(A,B)
print(C)

# Salida
[[ 89 107]
 [ 47 49]
 [ 40 44]]

Observe cómo este método es más sencillo que los dos métodos que aprendimos anteriormente. De hecho, en lugar de np.matmul(), puede utilizar un operador @ equivalente, y lo veremos enseguida.

Cómo utilizar el operador @ en Python para multiplicar matrices

En Python, @ es un operador binario utilizado para la multiplicación de matrices.

Opera sobre dos matrices y, en general, sobre matrices NumPy de N dimensiones, y devuelve la matriz producto.

Nota: Necesita tener Python 3.5 y posterior para utilizar el operador @.

He aquí cómo puede utilizarlo.

C = A@B
print(C)

# Salida
array([ 89, 107],
       [ 47, 49],
       [ 40, 44]])

Observe que la matriz producto C es la misma que la que obtuvimos anteriormente.

¿Puede utilizar np.dot() para multiplicar matrices?

Si alguna vez se ha encontrado con código que utiliza np.dot( ) para multiplicar dos matrices, a continuación le explicamos cómo funciona.

C = np.dot(A,B)
print(C)

# Salida
[[ 89 107]
 [ 47 49]
 [ 40 44]]

Verá que np.dot(A, B) también devuelve la matriz producto esperada.

Sin embargo, según la documentación de NumPy, debe utilizar np. dot() sólo para calcular el producto punto de dos vectores unidimensionales y no para la multiplicación de matrices.

Recordemos de la sección anterior que el elemento en el índice (i, j) de la matriz producto C es el producto escalar de la fila i de la matriz A y la columna j de la matriz B.

Como NumPy difunde implícitamente esta operación de producto punto a todas las filas y todas las columnas, obtendrá la matriz producto resultante. Pero para mantener su código legible y evitar ambigüedades, utilice en su lugar np.matmul() o el operador @.

Conclusión

🎯 En este tutorial, ha aprendido lo siguiente.

• Condición para que la multiplicación de matrices sea válida: número de columnas de la matriz A = número de filas de la matriz B.
• Cómo escribir una función personalizada de Python que compruebe si la multiplicación de matrices es válida y devuelva la matriz producto. El cuerpo de la función utiliza bucles for anidados.
• A continuación, ha aprendido a utilizar comprensiones de listas anidadas para multiplicar matrices. Son más sucintas que los bucles for pero son propensas a problemas de legibilidad.
• Por último, aprendió a utilizar la función incorporada a NumPy np.matmul() para multiplicar matrices y cómo ésta es la más eficiente en términos de velocidad.
• También aprendió sobre el operador @ para multiplicar dos matrices en Python.

Y con esto terminamos nuestra discusión sobre la multiplicación de matrices en Python. Como siguiente paso, aprenda a comprobar si un número es primo en Python. O resuelva problemas interesantes sobre cadenas en Python.

Feliz aprendizaje!🎉