Este tutorial le enseñará cómo imprimir el triángulo de Pascal en Python para un número determinado de filas.

Comenzará aprendiendo a construir el triángulo de Pascal. Después procederá a escribir una función en Python y aprenderá a optimizarla aún más.

▶️ ¡Empecemos!

¿Qué es el triángulo de Pascal y cómo construirlo?

La impresión del triángulo de Pascal para un número determinado de filas es una pregunta popular en las entrevistas.

En el triángulo de Pascal con n filas, la fila número i tiene i elementos.

Por tanto, la primera fila tiene un elemento, y es 1. Y cada elemento de las filas siguientes es la suma de los dos números situados justo encima.

La siguiente figura explica cómo construir el triángulo de Pascal con cinco filas.

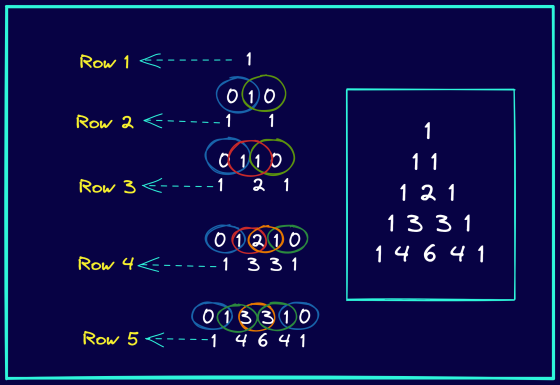
pascal-triangle-python
Triángulo de Pascal para numRows = 5 (Imagen del autor)

Observe cómo puede rellenar ceros cuando sólo tiene un número por encima de un determinado número.

📝Como ejercicio rápido, siga el procedimiento anterior para construir el triángulo de Pascal para n = 6 y n = 7.

A continuación, procedamos a escribir algo de código. Puede optar por ejecutar los fragmentos de código en el IDE de Python de Geekflare directamente desde su navegador- a medida que avanza en el tutorial.

Función Python para Imprimir el Triángulo de Pascal

En esta sección, vamos a escribir una función Python para imprimir el triángulo de Pascal para cualquier número dado de filas.

Hay dos cuestiones clave a tener en cuenta:

  • ¿Cómo expresar las entradas del triángulo de Pascal?
  • ¿Cómo imprimir el triángulo de Pascal con el espaciado y el formato adecuados?

Respondámoslas ahora.

#1. ¿Cuál es la expresión de cada entrada del triángulo de Pascal?

Resulta que las entradas del triángulo de Pascal se pueden obtener utilizando la fórmula para nCr. Si lo recuerda de sus matemáticas escolares, nCr denota el número de formas en que se pueden elegir r elementos de un conjunto de n elementos.

La fórmula para nCr se da a continuación:

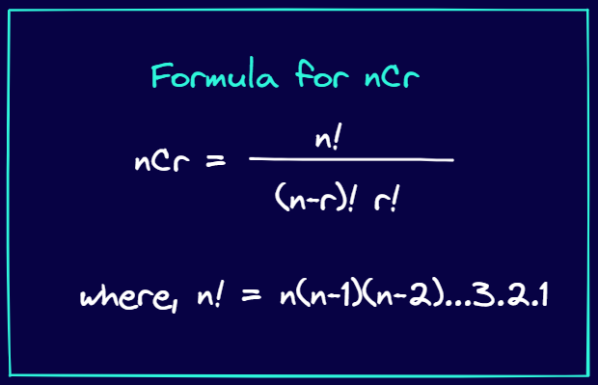
ncr-formula
fórmula nCr (Imagen del autor)

Ahora procedamos a expresar las entradas del triángulo de Pascal utilizando la fórmula nCr.

pascal-triangle-ncr-formula
Entradas del triángulo de Pascal utilizando nCr (Imagen del autor)

Ya hemos encontrado la forma de expresar las entradas de la matriz.

#2. ¿Cómo ajustar el espaciado al imprimir el patrón?

En el triángulo de Pascal con numRows, la fila #1 tiene una entrada, la fila #2 tiene dos entradas, y así sucesivamente. Para imprimir el patrón como un triángulo, necesitará numRows - i espacios en la fila #i. Y para ello puede utilizar la función range de Python junto con el bucle for.

Como la función range excluye por defecto el punto final, asegúrese de añadir 1 para obtener el número necesario de espacios iniciales.

Ahora que ha aprendido a representar entradas y también a ajustar el espacio mientras imprime el triángulo de Pascal, sigamos adelante y definamos la función pascal_tri.

Análisis sintáctico de la definición de la función

¿Qué quiere que haga la función pascal_tri?

  • La función pascal_tri debería aceptar el número de filas(numFilas) como argumento.
  • Debería imprimir el triángulo de Pascal con numFilas.

Para calcular el factorial, utilicemos la función factorial del módulo matemático incorporado de Python.

▶️ Ejecute la siguiente celda de código para importar factorial y utilizarlo en su módulo actual.

from math import factorial

El fragmento de código siguiente contiene la definición de la función.

def pascal_tri(numFilas):
  '''Imprime el triángulo de Pascal con numFilas.'''
  for i in range(numFilas):
    # bucle para obtener los espacios iniciales
	  for j in range(numFilas-i 1):
		  print(end=" ")
    
    # bucle para obtener los elementos de la fila i
	  para j en rango(i 1):
		  # nCr = ¡n!/((n-r)!*r!)
		  print(factorial(i)//(factorial(j)*factorial(i-j)), end=" ")

	 # imprima cada fila en una nueva línea
	  print("\n")

La función funciona de la siguiente manera:

  • La función pascal_tri tiene un parámetro obligatorio numRows: el número de filas.
  • Hay numRows filas en total. Por cada fila i, añadimos numRows - i espacios iniciales antes de la primera entrada de la fila.
  • A continuación, utilizamos la fórmula nCr para calcular las entradas individuales. Para la fila i, las entradas son iCj donde j = {0,1,2,..,i}.
  • Observe que utilizamos // que realiza la división entera, ya que queremos que las entradas sean enteras.
  • Después de calcular todas las entradas de una fila, imprima la fila siguiente en una nueva línea.

🔗 Como hemos añadido un docstring, puede utilizar la función de ayuda incorporada de Python, o el atributo __doc__ para acceder al docstring de la función. El fragmento de código siguiente muestra cómo hacerlo.

help(pascal_tri)

# Salida
Ayuda sobre la función pascal_tri en el módulo __main__:

pascal_tri(numFilas)
    Imprime el triángulo de Pascal con numRows.

pascal_tri.__doc__

# Salida
Imprime el triángulo de Pascal con numRows.

Ahora vamos a llamar a la función con el número de filas como argumento.

pascal_tri(3)

# Salida
     1
    1 1
   1 2 1

Se imprimen las 3 primeras filas del triángulo de Pascal, como se esperaba.

Imprimir el triángulo de Pascal utilizando la recursión

En la sección anterior, identificamos la expresión matemática de cada entrada del triángulo de Pascal. Sin embargo, no utilizamos la relación entre las entradas de dos filas consecutivas.

De hecho, utilizamos la fila anterior para calcular las entradas de la fila posterior. ¿No podemos utilizar esto y llegar a una implementación recursiva de la función pascal_tri?

Sí, ¡hagámoslo!

En una implementación recursiva, una función se llama a sí misma repetidamente hasta que se cumple el caso base. En la construcción del triángulo de Pascal, empezamos con la primera fila con una entrada 1, y luego construimos las filas siguientes.

Así que la llamada a la función pascal_tri(numRows) llama a su vez a pascal_tri(numRows-1) y así sucesivamente, hasta que se alcanza el caso base pascal_tri(1).

Considere el ejemplo en el que necesita imprimir las 3 primeras filas del triángulo de Pascal. La siguiente imagen explica cómo las llamadas recursivas son empujadas a la pila. Y cómo las llamadas a funciones recursivas devuelven las filas del triángulo de Pascal.

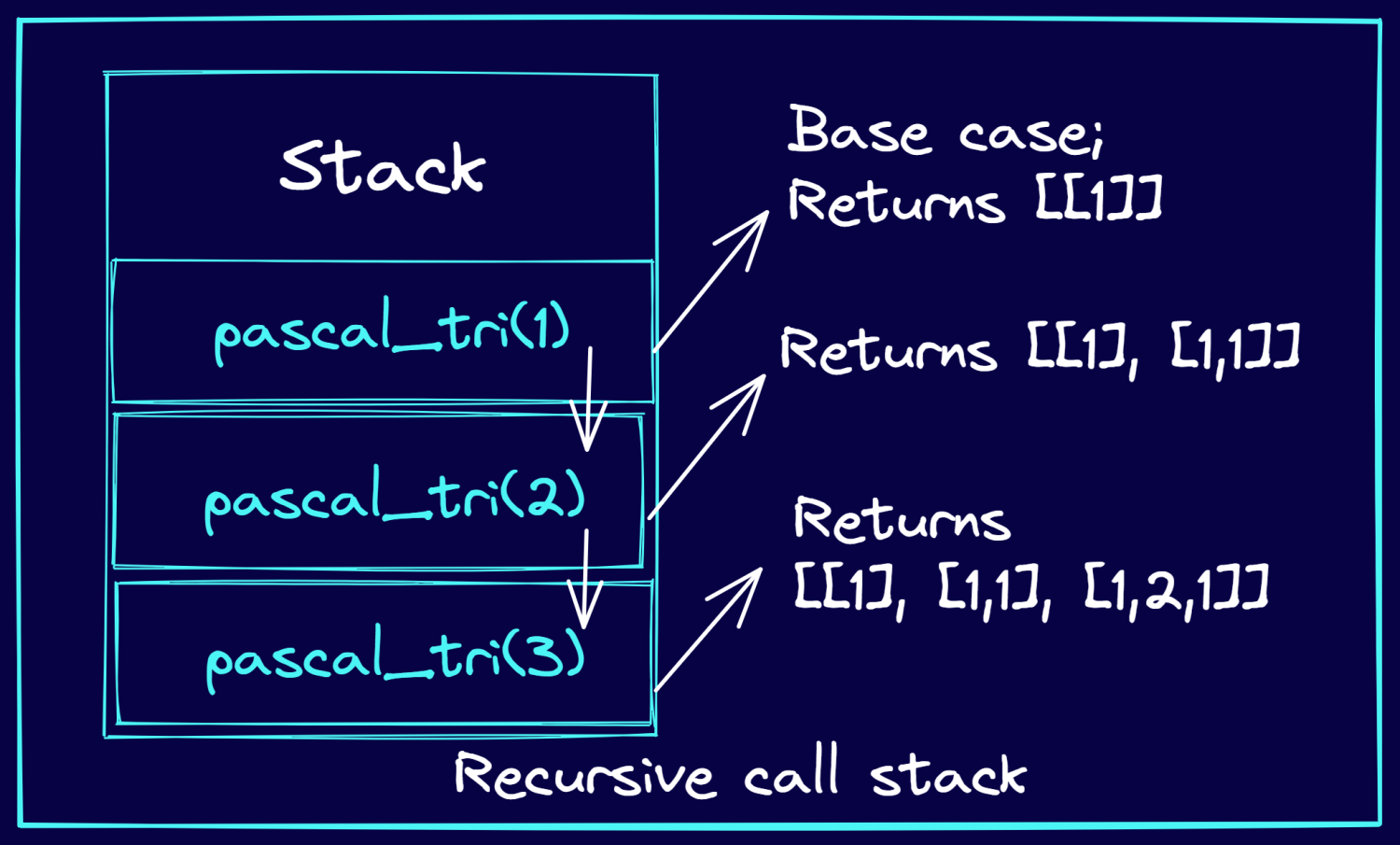
pascal-triangle-recursion
Pila de llamadas durante las llamadas recursivas (Imagen del autor)

▶️ Ejecute el fragmento de código siguiente para generar las filas del triángulo de Pascal de forma recursiva.

def pascal_tri(numFilas):
    '''Imprime el triángulo de Pascal con numRows.'''
    if numFilas == 1
        return [<x><x><x>[1]</x></x></x>] # ¡se alcanza el caso base!
    si no
        res_arr = pascal_tri(numRows-1) # llamada recursiva a pascal_tri
        # utilizar fila anterior para calcular fila actual 
        fila_actual = <x><x><x>[1]</x></x></x> # cada fila empieza por 1
        prev_row = res_arr[-1] 
        for i in range(len(prev_row)-1):
            # suma de las 2 entradas inmediatamente anteriores
            cur_row.append(prev_row<x><x>[i]</x></x> prev_row[i 1]) 
        fila_cur = <x><x><x>[1]</x></x></x> # cada fila termina con 1
        res_arr.append(cur_row)
        return res_arr

Aquí hay algunos puntos de los que merece la pena tomar nota:

  • Hemos utilizado una lista anidada como estructura de datos, en la que cada fila del triángulo de Pascal es una lista en sí misma, así [[fila 1], [fila 2],…,[fila n]].
  • La llamada a la función pascal_tri(numRows) desencadena una serie de llamadas recursivas con numRows - 1, numRows - 2 hasta llegar a 1 como argumentos. Estas llamadas se introducen en una pila.
  • Cuando numRows == 1, hemos alcanzado el caso base, y la función devuelve [[1]].
  • Ahora la lista devuelta es utilizada por las funciones posteriores en la pila de llamadas para calcular la siguiente fila.
  • Si cur_row es la fila actual, cur_row<x><x>[i]</x></x> = prev_row<x><x>[i]</x></x> prev_row[i 1]-la suma de 2 elementos directamente por encima del índice actual.

Como la matriz devuelta es una lista anidada (lista de listas), necesitamos ajustar el espaciado e imprimir las entradas, como se muestra en la celda de código siguiente.

tri_array = pascal_tri(5)

para i,fila en enumerar(tri_array):
  for j in range(len(tri_array) - i 1):
    print(end=" ") # espacios iniciales
  para j en fila
    print(j, end=" ") # imprimir entradas
  print("\n") # imprimir nueva línea

La salida es correcta, como se ve a continuación

# Salida

       1

      1 1

     1 2 1

    1 3 3 1

   1 4 6 4 1

Función de Python para imprimir el triángulo de Pascal para numRows ≤ 5

Ambos métodos que ha aprendido funcionarán para imprimir el triángulo de Pascal para un número arbitrario de filas numRows.

Sin embargo, hay ocasiones en las que necesita imprimir el triángulo de Pascal para un número menor de filas. Y cuando el número de filas que necesita imprimir es como máximo 5, puede utilizar una técnica sencilla.

Repase la siguiente figura. Y observe cómo las potencias de 11 son idénticas a las entradas del triángulo de Pascal. Además, observe que esto sólo funciona hasta la 4ª potencia de 11. Es decir, 11 elevado a las potencias {0, 1, 2, 3, 4} da las entradas de las filas 1 a 5 del triángulo de Pascal.

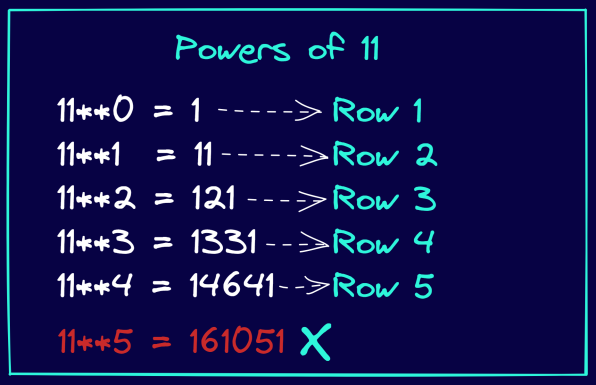
pascal-triangle-powers-of-11

Reescribamos la definición de la función, como se muestra a continuación:

def pascal_tri(numFilas):
  '''Imprime el triángulo de Pascal con numFilas.'''
  for i in range(numFilas):
    print(''*(numFilas-i), end='')
    # calcular la potencia de 11
    print(' '.join(str(11**i)))

He aquí cómo funciona la función pascal_tri:

  • Como en los ejemplos anteriores, ajustamos el espaciado.
  • Y después, utilizamos el operador de exponenciación de Python (**) para calcular las potencias de 11.
  • Como las potencias de 11 son números enteros por defecto, conviértalas en una cadena utilizando str(). Ahora tiene las potencias de 11 como cadenas.
  • Las cadenas en Python son iterables, por lo que puede hacer un bucle a través de ellas y acceder a un carácter cada vez.
  • A continuación, puede utilizar el método join () con la sintaxis: <sep>.join(<iterable>) para unir elementos en <iterable> utilizando <sep> como separador.
  • Aquí, se necesita un solo espacio entre los caracteres, por lo que <sep> será ' ', <iterable> es cadena: potencia de 11.

Comprobemos si la función funciona como es debido.

pascal_tri(5)

# Salida
     1
    1 1
   1 2 1
  1 3 3 1
 1 4 6 4 1

Como otro ejemplo, llame a la función pascal_tri con 4 como argumento.

pascal_tri(4)

# Salida
     1
    1 1
   1 2 1
  1 3 3 1

Espero que entienda cómo puede imprimir fácilmente el triángulo Pascal para numRows en el rango de 1 a 5.

Conclusión

Esto es lo que hemos aprendido

  • Cómo construir el triángulo de Pascal con el número de filas dado. Cada número de cada fila es la suma de los dos números situados justo encima.
  • Escribir una función Python utilizando la fórmula nCr = ¡n!/(n-r)!.r! para calcular las entradas del triángulo de Pascal.
  • A continuación, aprendió una implementación recursiva de la función.
  • Por último, aprendió el método más óptimo para construir el triángulo de Pascal para numRows hasta 5-utilizando las potencias de 11.

Si quiere mejorar sus conocimientos de Python, aprenda a multiplicar matrices, a comprobar si un número es primo y a resolver problemas sobre operaciones con cadenas. ¡Feliz codificación!