Implementar la búsqueda es siempre un reto, pero no imposible.
En la vida real, buscaremos sin seguir ningún patrón. Simplemente vamos a los lugares en los que creemos que puede estar. No seguimos ningún patrón en la mayoría de los casos.
¿Funciona lo mismo en el mundo de la programación?
No! tiene que haber algún patrón para buscar cosas en los programas. Vamos a ver algunos algoritmos que siguen diferentes patrones para buscar en este artículo.
Hay múltiples algoritmos que podemos encontrar en el mundo de la programación. Vamos a discutir los algoritmos más importantes y más utilizados en este artículo. Y el resto de los algoritmos será pan comido para usted aprenderlos.
Buscar se refiere a buscar un elemento en el array en este artículo.
Veámoslos uno a uno.
Búsqueda lineal
El nombre sugiere que el algoritmo de búsqueda line al sigue elpatrón lineal para buscar los elementos de una matriz. El algoritmo empieza a buscar el elemento desde el principio de la matriz y se desplaza hacia el final hasta que encuentra el elemento. Detiene la ejecución del programa cuando encuentra el elemento requerido.
Vamos a ilustrar los algoritmos de búsqueda lineal con algunas ilustraciones interesantes para una mejor comprensión del algoritmo.
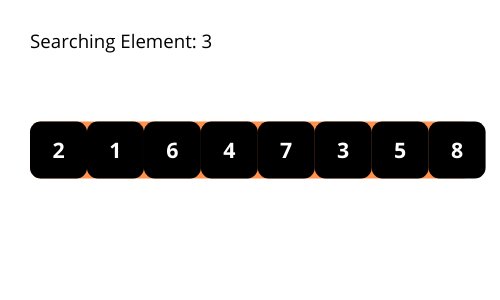
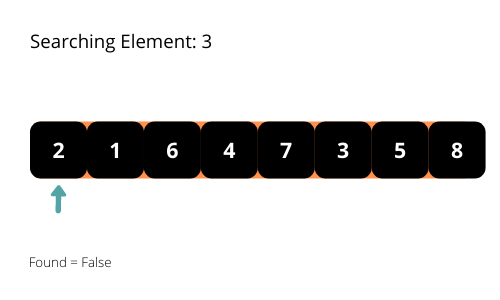
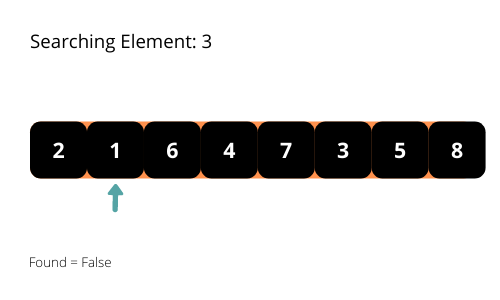
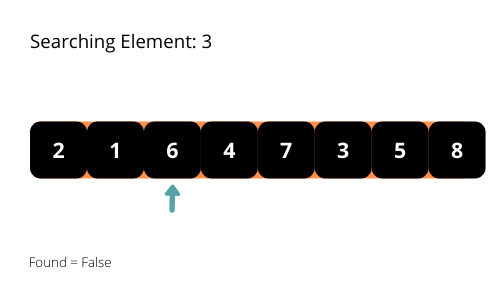
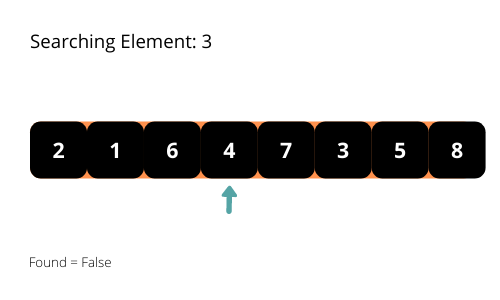
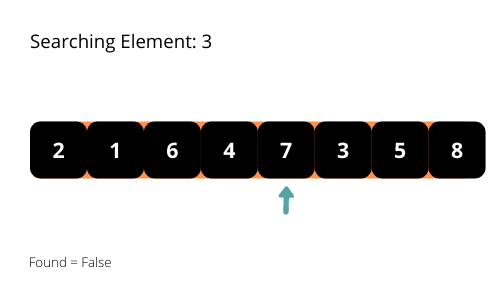
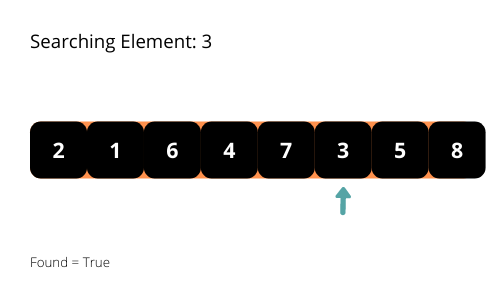
Si observa detenidamente el patrón de búsqueda, comprobará que el tiempo de ejecución del programa será O(n) en el peor de los casos. Tenemos que considerar la complejidad temporal en el peor de los casos de los algoritmos a analizar. Por lo tanto, la complejidad temporal del algoritmo es O (n).
Veamos la implementación del algoritmo de búsqueda lineal.
Implementación de la búsqueda lineal
Ahora, usted tiene una buena comprensión del algoritmo de búsqueda lineal. Es hora de ensuciarnos las manos con algo de código. Veamos primero los pasos para implementar la búsqueda lineal. A continuación, intente codificarla. No se preocupe aunque no pueda; le proporcionaré el código después.
Veamos los pasos para implementar el algoritmo de búsqueda lineal.
- Inicialice una matriz de elementos (sus números de la suerte).
- Escriba una función llamada buscar_elemento , que acepte tres argumentos, array, longitud del array y elemento a buscar.
- buscar_elemento(arr, n, elemento):
- Itere sobre la matriz dada.
- Comprueba si el elemento actual es igual al elemento buscado.
- En caso afirmativo, devuelve True.
- Después de completar el bucle, si la ejecución sigue en la función, entonces el elemento no está presente en el array. Por lo tanto devuelve False.
- Itere sobre la matriz dada.
- Imprima el mensaje basado en el valor de retorno de la función buscar_elemento.
Por último, escriba el código con la ayuda de los pasos anteriores para implementar el algoritmo de búsqueda lineal.
¿Ha completado la implementación del algoritmo de búsqueda lineal? Espero que sí. Si lo ha completado, compruébelo con el siguiente código.
Si no lo completó, no se preocupe,; vea el siguiente código y aprenda cómo lo implementamos. Lo conseguirá sin mucho esfuerzo.
## función de búsqueda
def buscar_elemento(arr, n, elemento):
## iterando a través del array
for i in range(n):
## comprobando el elemento actual con el elemento requerido
if arr[i] == elemento
## devolviendo True en caso de coincidencia
devolver True
## no se encuentra el elemento de ahí que la ejecución venga aquí
devolver Falso
if __name__ == '__main__':
## inicializar el array, la longitud y el elemento a buscar
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
n = 10
elemento_a_buscar = 6
# elemento_a_buscar = 11
if buscar_elemento(arr, n, elemento_a_buscar):
print(elemento_a_buscar, "se ha encontrado")
si no
print(elemento_a_buscar, "no se encuentra")
Primero, ejecute el programa con un elemento que esté presente en la matriz. Y a continuación, ejecútelo con un elemento que no esté presente en la matriz.
La complejidad temporal del algoritmo de búsqueda lineal es O(n).
¿Podemos reducirla un poco más con diferentes patrones?
Sí, podemos. Veámoslo.
Búsqueda binaria
El algoritmo de búsqueda binaria comprueba siempre el elemento central de la matriz. Este algoritmo busca el elemento en una matriz ordenada.
El algoritmo de búsqueda binaria itera sobre la matriz y comprueba el elemento del medio, si lo encuentra, entonces detiene el programa. Si el elemento medio es menor que el elemento requerido, entonces omite la parte izquierda de la matriz del elemento medio de la búsqueda. Si el elemento central es mayor que el elemento requerido, omite la parte derecha de la matriz del elemento central de la búsqueda.
En cada iteración, el algoritmo de búsqueda binaria reduce el área de búsqueda del elemento. Así, el número de comprobaciones es menor que el número de comprobaciones realizadas en el algoritmo de búsqueda lineal.
Las ilustraciones nos ayudan a comprender mejor el algoritmo de búsqueda binaria. Vamos a verlas.
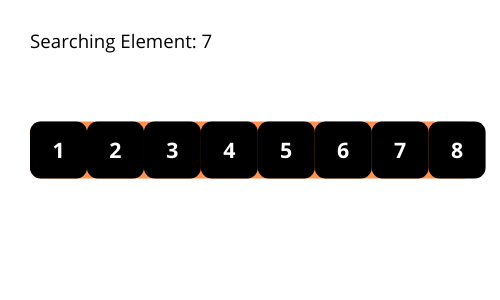
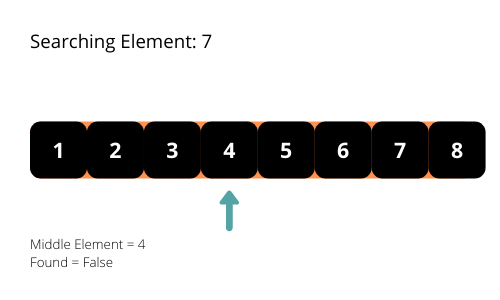
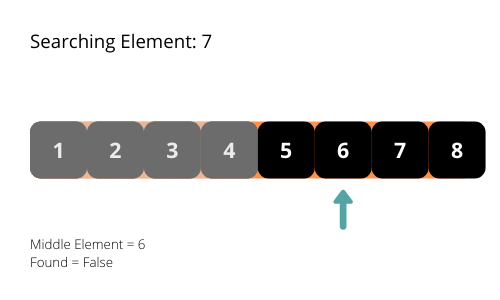
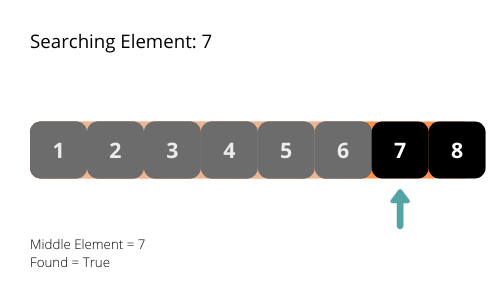
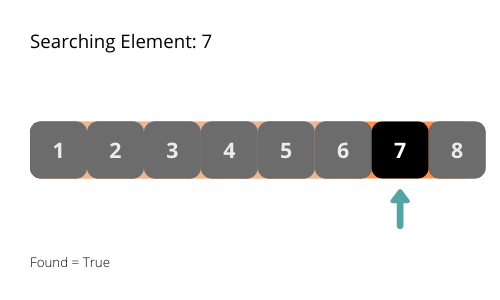
La complejidad temporal del algoritmo de búsqueda binaria es O(log n). En cada iteración, la longitud del área de búsqueda se reduce a la mitad. Se reduce exponencialmente.
Implementación de la búsqueda binaria
Primero veremos los pasos para implementar el algoritmo de búsqueda binaria y después el código. Veamos los pasos para completar la implementación del algoritmo de búsqueda binaria.
- Inicialice la matriz con elementos (sus números de la suerte)
- Escriba una función llamada buscar_elemento , que acepte tres argumentos, matriz ordenada, longitud de la matriz y elemento a buscar.
- buscar_elemento(matriz_ordenada, n, elemento):
- Inicialice la variable de índice i para la iteración del array.
- A continuación, inicialice dos variables para mantener el área de búsqueda del array. Aquí las llamamos inicio y fin porque indican índices.
- Itere hasta que i sea menor que la longitud del array.
- Calcule el índice medio del área de búsqueda utilizando los valores de inicio y fin . Será (inicio fin) // 2.
- Compruebe si el elemento indexado del medio de la zona de búsqueda es igual al elemento requerido o no.
- En caso afirmativo, devolverá True.
- De lo contrario, si el elemento indexado del medio es menor que el elemento requerido, entonces mueva el índice de inicio del área de búsqueda al medio 1.
- Else si el elemento indexado medio es mayor que el elemento requerido, entonces mueva el índice final del área de búsqueda a medio – 1.
- Incremente el índice de la matriz i.
- Después de completar el bucle, si la ejecución sigue en la función, entonces el elemento no está presente en el array. Por lo tanto devuelve False.
- Imprima el mensaje basado en el valor de retorno de la función buscar_elemento.
Intente escribir el código de forma similar a la implementación del algoritmo de búsqueda lineal.
…
¿Ha conseguido el código?
Sí, compárelo con el código de abajo. No, no se preocupe; entienda la implementación con el código de abajo.
## función de búsqueda
def buscar_elemento(ordenar_arr, n, elemento):
## índice del array para la iteración
i = 0
## variables para seguir la zona de búsqueda
## inicializándolas con los índices de inicio y fin
inicio = 0
fin = n - 1
## iterar sobre la matriz
while i < n
## obteniendo el índice del elemento medio
medio = (inicio fin) // 2
## comprobar el elemento medio con el elemento requerido
if sorted_arr[middle] == elemento:
## devolviendo True ya que el elemento está en el array
devolver True
elif sorted_arr[ middle] < element:
## moviendo el índice de inicio de la zona de búsqueda a la derecha
inicio = medio 1
else:
## mover el índice final del área de búsqueda a la izquierda
fin = medio - 1
i = 1
devolver Falso
if __name__ == '__main__':
## inicializar el array, la longitud y el elemento a buscar
arr = [1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
n = 10
elemento_a_buscar = 9
# elemento_a_buscar = 11
if buscar_elemento(arr, n, elemento_a_buscar):
print(elemento_a_buscar, "se ha encontrado")
si no
print(elemento_a_buscar, "no se encuentra")
Pruebe el código con diferentes casos en los que el elemento esté presente y no lo esté en algunos casos.
Conclusión
El algoritmo de búsqueda binaria es mucho más eficiente que el algoritmo de búsqueda lineal. Necesitamos ordenar el array para el algoritmo de búsqueda binaria no es el caso en el algoritmo de búsqueda lineal. La ordenación requiere cierto tiempo. Pero, el uso de algoritmos eficientes para la ordenación formará una buena combinación con el algoritmo de búsqueda binaria.
Ahora, usted tiene un buen conocimiento de los algoritmos más utilizados en Python.
A continuación, descubra algunos de los programas de búsqueda autoalojados más populares.
Feliz codificación 🙂 🧑💻

