Depuis la première idée d’un ordinateur quantique en 1980 jusqu’à aujourd’hui, le secteur de l’informatique quantique s’est considérablement développé, en particulier au cours des dix dernières années. De nombreuses entreprises travaillent sur des ordinateurs quantiques.
À la fin de cet article, vous comprendrez ce qu’est l’informatique quantique, les différents types d’informatique quantique, leur fonctionnement, leurs algorithmes, leurs modèles, leurs approches, leurs défis et leurs applications.
Qu’est-ce que l’ordinateur quantique ?
L’ordinateur quantique résout les problèmes différemment des ordinateurs qui nous sont familiers et que je qualifierai désormais d’ordinateurs classiques.
Les ordinateurs quantiques présentent certains avantages par rapport aux ordinateurs normaux pour certains problèmes, qui proviennent de leur capacité à se trouver dans un très grand nombre d’états en même temps, alors que les ordinateurs classiques ne peuvent occuper qu’un seul état à la fois.

Pour comprendre cela, et pour comprendre comment fonctionnent les ordinateurs quantiques, vous devez comprendre trois choses : La superposition, l’intrication et l’interférence.
Les bases d’un ordinateur ordinaire sont des bits, et pour un ordinateur quantique, ce sont des bits quantiques ou qubits en abrégé. Ils fonctionnent de manière fondamentalement différente.
Un bit classique est comme un interrupteur qui peut être soit un 0, soit un 1, ce que vous connaissez probablement déjà sous le nom d’information binaire. Lorsque nous mesurons un bit, nous obtenons simplement l’état dans lequel il se trouve actuellement, mais nous verrons que ce n’est pas le cas des qubits. Un qubit est plus compliqué.
Superposition
Pour une visualisation utile, vous pouvez les considérer comme une flèche pointant dans l’espace 3D. Si la flèche pointe vers le haut, elle est dans l’état 1 et si elle pointe vers le bas, elle est dans l’état 0, tout comme un bit classique, mais elle peut également se trouver dans un état de superposition, c’est-à-dire lorsque la flèche pointe dans n’importe quelle autre direction.
Cet état de superposition est une combinaison de 0 et de 1.

Lorsque vous mesurez un qubit, le résultat est toujours 1 ou 0, mais la probabilité d’obtenir l’un ou l’autre dépend de la direction de la flèche.
Si la flèche pointe vers le haut, vous avez plus de chances d’obtenir un 1 qu’un 0, et si elle pointe vers le bas, vous avez plus de chances d’obtenir un 0 qu’un 1, et si elle est exactement sur l’équateur, vous obtiendrez l’un ou l’autre état avec une probabilité de 50 %.
Voilà donc expliqué l’effet de la superposition ; passons maintenant à l’intrication.
L’intrication
Dans les ordinateurs classiques, les bits sont entièrement indépendants les uns des autres. L’état d’un bit n’est pas influencé par l’état des autres bits. Mais dans les ordinateurs quantiques, les qubits peuvent être intriqués les uns avec les autres, ce qui signifie qu’ils deviennent ensemble une partie d’un grand état quantique.
Prenons l’exemple de deux qubits qui se trouvent chacun dans un état de superposition différent, mais qui ne sont pas encore intriqués. Vous pouvez voir les probabilités à côté d’eux, et ces probabilités sont actuellement indépendantes l’une de l’autre.
Mais lorsque nous les intriquons, nous devons nous débarrasser de ces probabilités indépendantes et calculer une distribution de probabilités de tous les états possibles que nous pouvons obtenir. Soit 00, 01, 10 ou 11.

Le point important ici est que les qubits sont intriqués ; si vous changez la direction de la flèche sur un qubit, cela modifie la distribution de probabilité pour l’ensemble du système, de sorte que les qubits ne sont plus indépendants les uns des autres ; ils font tous partie du même grand état.
Et ce, quel que soit le nombre de qubits que vous possédez. Vous noterez également que pour un qubit, vous disposez d’une distribution de probabilité sur deux états.
Avec deux qubits, vous avez une distribution de probabilités répartie sur quatre états. Pour trois qubits, vous avez une distribution sur 8 états, et cela continue à doubler chaque fois que vous ajoutez un autre qubit.
En général, un ordinateur quantique de n qubits peut se trouver dans une combinaison de 2^n états. Je dirais donc qu’il s’agit là de la principale différence entre les ordinateurs classiques et les ordinateurs quantiques.

Les ordinateurs classiques peuvent être dans tous les états que vous voulez, mais ils ne peuvent être que dans un seul état à la fois, alors que les ordinateurs quantiques peuvent être dans une superposition de tous ces états en même temps.
Mais vous vous demandez peut-être en quoi le fait d’être dans cet état de superposition peut être utile à un ordinateur. Pour cela, nous avons besoin de la dernière composante : L’interférence.
L’interférence
Pour expliquer l’effet de l’interférence, nous devons revenir en arrière et regarder mon image d’un qubit, techniquement appelé sphère de Bloch. Un qubit ne ressemble pas à cela ; il s’agit simplement d’une belle façon de visualiser l’état d’un qubit.
En réalité, l’état d’un qubit est décrit par une entité plus abstraite appelée fonction d’onde quantique. Les fonctions d’onde sont la description mathématique fondamentale de tout ce qui se passe en mécanique quantique.
Lorsque plusieurs qubits sont intriqués, toutes leurs fonctions d’onde sont additionnées pour former une fonction d’onde globale décrivant l’état de l’ordinateur quantique.
Cette addition des fonctions d’onde constitue l’interférence car, comme pour les ondulations de l’eau, lorsque l’on additionne des ondes, celles-ci peuvent interférer de manière constructive et s’additionner pour former une onde plus grande, ou interférer de manière destructive pour s’annuler mutuellement.

La fonction d’onde globale de l’ordinateur quantique est ce qui définit les différentes probabilités des différents états, et en changeant les états des différents qubits, nous pouvons changer les probabilités que différents états soient révélés lorsque nous mesurons l’ordinateur quantique.
N’oubliez pas que même si l’ordinateur quantique peut se trouver dans une superposition de millions d’états en même temps lorsque nous le mesurons, nous n’obtenons qu’un seul état.
Ainsi, lorsque vous utilisez un ordinateur quantique pour résoudre un problème de calcul, vous devez utiliser l’interférence constructive pour augmenter la probabilité de la bonne réponse, et utiliser l’interférence destructive pour diminuer les probabilités des mauvaises réponses afin que, lorsque vous le mesurez, la bonne réponse apparaisse.
Algorithmes quantiques
La manière dont vous procédez relève du domaine des algorithmes quantiques, et toute la motivation derrière l’informatique quantique est que, théoriquement, il y a un tas de problèmes que vous pouvez résoudre sur un ordinateur quantique et qui sont considérés comme insolubles sur des ordinateurs classiques.
Jetons-y un coup d’œil. Il existe de nombreux algorithmes quantiques, trop nombreux pour être décrits dans cet article. Nous nous concentrerons donc sur le plus célèbre et le plus important d’un point de vue historique : l’algorithme de Shor.
#1. Algorithme de Shor
Si vous avez deux grands nombres et que vous les multipliez ensemble, il existe un algorithme classique très rapide et efficace pour trouver la réponse. Cependant, si vous partez de la réponse et que vous vous demandez quels sont les nombres originaux qui se multiplient pour former ce nombre, la tâche est beaucoup plus difficile C’est beaucoup plus difficile.
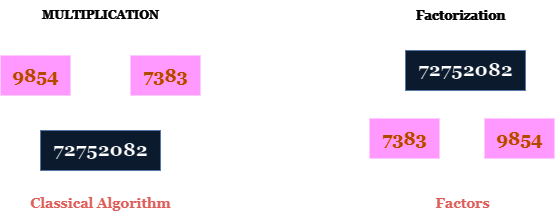
C’est ce qu’on appelle la factorisation, et ces nombres sont appelés facteurs. La raison pour laquelle il est si difficile de les trouver est que l’espace de recherche des facteurs possibles est très vaste. Il n’existe pas d’algorithme classique efficace pour trouver les facteurs des grands nombres.
C’est pourquoi nous utilisons cette propriété mathématique pour le cryptage de l’internet : sécurisation des sites web, des courriels et des comptes bancaires. Si vous connaissez ces facteurs, vous pouvez facilement décrypter les informations, mais si vous ne les connaissez pas, vous devez d’abord les trouver, ce qui est impossible à réaliser avec les ordinateurs les plus puissants du monde.

C’est pourquoi, en 1994, la publication par Peter Shor d’un algorithme quantique rapide capable de trouver efficacement les facteurs de grands nombres entiers a fait grand bruit.
C’est à ce moment-là que beaucoup de gens ont commencé à prendre l’idée de l’informatique quantique au sérieux, car il s’agissait de la première application à un problème réel ayant potentiellement d’énormes implications en matière de sécurité dans le monde réel.
Mais lorsque je parle d’algorithme quantique “rapide”, à quelle vitesse et de combien serait-il plus rapide qu’un ordinateur classique ? Pour répondre à ces questions, nous devons faire un petit détour par le monde de la théorie de la complexité quantique.
La théorie de la complexité quantique
La théorie de la complexité quantique est un sous-domaine de la théorie de la complexité informatique, qui traite de la catégorisation des algorithmes, en les classant dans des catégories en fonction de leur efficacité sur les ordinateurs.
La classification est déterminée par le niveau croissant de difficulté à résoudre le problème à mesure qu’il devient plus grand. Ici, tout problème situé dans la boîte P est facile à résoudre pour les ordinateurs classiques, mais tout problème situé en dehors de cette boîte signifie que nous ne disposons pas d’algorithmes classiques efficaces pour le résoudre, et la factorisation des grands nombres est l’un de ces problèmes.
Mais il existe un cercle, BQP, qui est efficace pour un ordinateur quantique mais pas pour un ordinateur classique. Ce sont ces problèmes que les ordinateurs quantiques parviendront à résoudre mieux que les ordinateurs classiques.
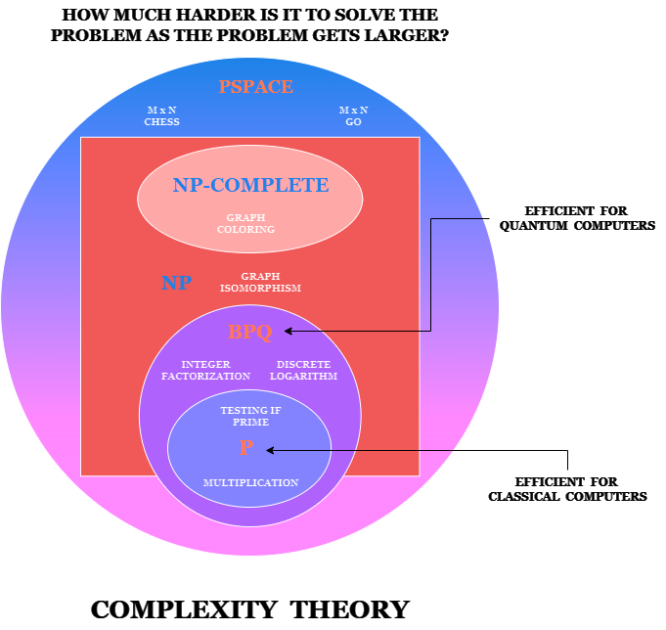
Comme je l’ai dit, la théorie de la complexité s’intéresse à la difficulté de résoudre un problème à mesure que celui-ci prend de l’ampleur. Ainsi, si vous factorisez un nombre à 8 chiffres, puis que vous ajoutez un autre chiffre, à quel point est-il plus difficile de factoriser le nouveau nombre que l’ancien ? Est-ce deux fois plus difficile ?
Exponentiellement plus difficile ? Et quelle est la tendance au fur et à mesure que vous ajoutez des chiffres ? C’est ce qu’on appelle la complexité ou la mise à l’échelle, et pour la factorisation, elle est exponentielle.
Tout ce qui comporte un N dans l’exposant est exponentiellement difficile. Dans le monde de l’informatique, vous pouvez gagner respect et renommée si vous trouvez un meilleur algorithme pour résoudre ces problèmes les plus difficiles.
L’algorithme de Shor en est un exemple : il a tiré parti des caractéristiques particulières des ordinateurs quantiques pour créer un algorithme capable de résoudre la factorisation des nombres entiers avec une échelle bien meilleure que celle du meilleur algorithme classique.
Le meilleur algorithme classique est exponentiel, alors que l’algorithme de Shor est polynomial, ce qui est énorme dans le monde de la théorie de la complexité et de l’informatique en général, car cela transforme un problème insoluble en un problème soluble
Résolu, c’est-à-dire si vous disposez d’un ordinateur quantique fonctionnel, ce que l’on s’efforce de construire. Mais vous ne devez pas encore vous inquiéter pour la sécurité de votre compte en banque, car les ordinateurs quantiques actuels ne sont pas encore capables d’exécuter l’algorithme de Shor sur de grands nombres.
Ils auraient besoin d’un grand nombre de qubits pour y parvenir, mais jusqu’à présent, les ordinateurs quantiques universels les plus avancés en ont environ 433.
Par ailleurs, des chercheurs travaillent sur ce que l’on appelle les systèmes de cryptage post-quantique, qui n’utilisent pas la factorisation des nombres entiers, et une autre technologie issue du monde de la physique quantique peut également être utile à cet égard, un système de cryptographie connu sous le nom de cryptographie quantique.
Il s’agit là d’un algorithme quantique parmi d’autres, mais il en existe beaucoup d’autres, chacun offrant des niveaux d’accélération différents.
#2. L’algorithme de Grover
Un autre exemple notable est l’algorithme de Grover, qui peut rechercher des listes de données non structurées plus rapidement que le meilleur algorithme classique.
Il convient toutefois de veiller à ne pas mal caractériser les ordinateurs classiques. Ce sont des appareils très polyvalents, et rien ne dit que quelqu’un pourrait trouver un algorithme classique très intelligent capable de résoudre plus efficacement les problèmes les plus difficiles, comme la factorisation des nombres entiers.
Les gens pensent que c’est très peu probable, mais ce n’est pas exclu. Par ailleurs, il existe des problèmes dont nous pouvons prouver qu’ils sont impossibles à résoudre sur des ordinateurs classiques, appelés problèmes non calculables, comme le problème de l’arrêt, mais ils sont également impossibles à résoudre sur un ordinateur quantique.
Sur le plan informatique, les ordinateurs classiques et les ordinateurs quantiques sont donc équivalents, les différences venant des algorithmes qu’ils peuvent exécuter. Vous pouvez même simuler un ordinateur quantique sur un ordinateur classique et vice versa.
La simulation d’un ordinateur quantique sur un ordinateur classique devient exponentiellement plus difficile à mesure que le nombre de qubits simulés augmente.
En effet, les ordinateurs classiques ont du mal à simuler des systèmes quantiques, mais les ordinateurs quantiques étant déjà des systèmes quantiques, ils n’ont pas ce problème, ce qui m’amène à mon application préférée des ordinateurs quantiques : la simulation quantique.
#3. Simulation quantique
La simulation quantique consiste à simuler des choses telles que des réactions chimiques ou la manière dont les électrons se comportent dans différents matériaux à l’aide d’un ordinateur. Dans ce domaine, les ordinateurs quantiques ont également une vitesse exponentielle par rapport aux ordinateurs classiques, car ces derniers ont du mal à simuler les systèmes quantiques.
Mais simuler des systèmes quantiques avec aussi peu de particules est difficile, même sur les superordinateurs les plus puissants du monde. Nous ne pouvons pas encore le faire sur les ordinateurs quantiques, mais à mesure qu’ils mûrissent, l’un des principaux objectifs est de simuler des systèmes quantiques de plus en plus grands.
Il s’agit notamment de domaines tels que le comportement de matériaux exotiques à basse température, la compréhension de la supraconductivité de certains matériaux ou l’étude de réactions chimiques importantes en vue d’en améliorer l’efficacité ; un exemple vise à produire des engrais de manière à émettre beaucoup moins de dioxyde de carbone, la production d’engrais contribuant à environ 2 % des émissions mondiales de carbone.
Vous pouvez en savoir plus sur la simulation de la chimie quantique.
Parmi les autres applications potentielles de la simulation quantique, citons l’amélioration des panneaux solaires et des batteries, ainsi que la mise au point de nouveaux médicaments, produits chimiques ou matériaux pour l’aérospatiale.
En général, la simulation quantique signifie que nous pourrions rapidement créer des prototypes de nombreux matériaux différents à l’intérieur d’un ordinateur quantique et tester tous leurs paramètres physiques au lieu de devoir les fabriquer physiquement et les tester en laboratoire, ce qui est un processus beaucoup plus laborieux et coûteux.
Cela pourrait permettre d’accélérer considérablement les processus et de réaliser des économies substantielles de temps et d’argent. Il convient de rappeler qu’il s’agit là d’applications potentielles des ordinateurs quantiques, car nous ne disposons pas encore d’ordinateurs quantiques capables de résoudre les problèmes du monde réel mieux que nos ordinateurs normaux. Mais ce sont les types de problèmes pour lesquels les ordinateurs quantiques seraient bien adaptés.
Modèles d’ordinateurs quantiques

Dans le monde des ordinateurs quantiques, il existe un large éventail d’approches pour transformer différents types de systèmes quantiques en ordinateurs quantiques, et il y a deux niveaux de nuance dont je dois parler.
Le modèle du circuit
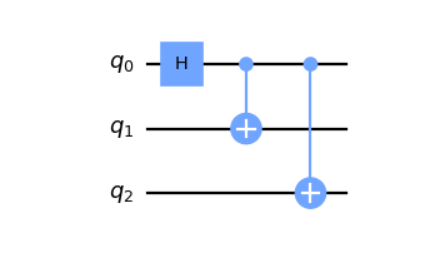
Dans le modèle du circuit, il y a des qubits qui fonctionnent ensemble et des portes spéciales qui modifient quelques qubits à la fois, changeant leur état sans vérification. Ils placent ces portes dans un ordre spécifique pour créer un algorithme quantique. Enfin, ils mesurent les qubits pour obtenir la réponse souhaitée.
Informatique quantique adiabatique
Dans le calcul quantique adiabatique, vous tirez parti de l’un des comportements fondamentaux de la physique, à savoir le fait que tout système physique évolue toujours vers l’état d’énergie minimale. Le calcul quantique adiabatique fonctionne en formulant les problèmes de telle sorte que l’état d’énergie le plus bas du système quantique représente la solution.
Recuit quantique
Le recuit quantique n’est pas un schéma universel de calcul quantique, mais il fonctionne sur le même principe que le calcul quantique adiabatique, le système trouvant l’état d’énergie minimum d’un paysage énergétique que vous lui donnez.
Calcul quantique topologique
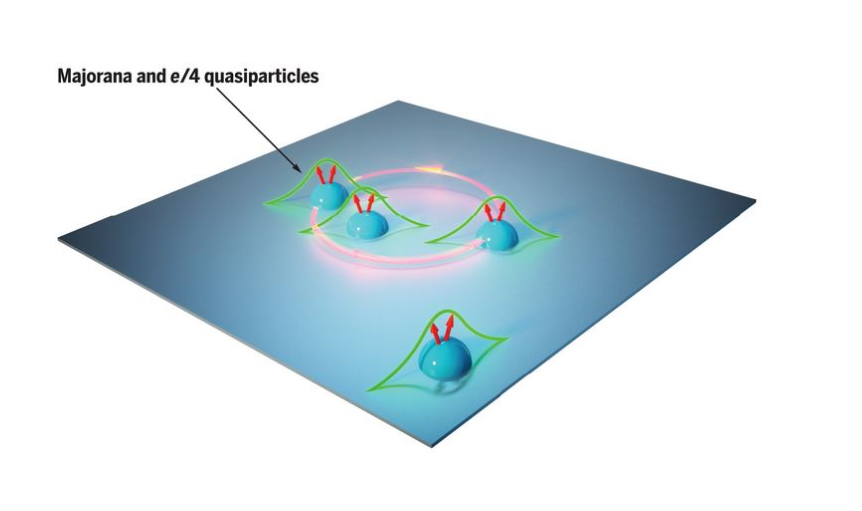
Dans cette approche, les qubits sont construits à partir d’une entité physique appelée quasi-particule de Majorana à mode zéro, qui est un type d’anyon non abélien. Ces quasi-particules devraient être plus stables en raison de leur séparation physique.
Les défis de la construction
Quelle que soit l’approche retenue, elle se heurte à une série d’obstacles similaires, qu’il convient d’examiner en premier lieu.
- Décohérence : Il est très difficile de contrôler les systèmes quantiques, car la moindre interaction avec le monde extérieur entraîne une fuite de l’information. C’est ce qu’on appelle la décohérence. Vos qubits seront constitués d’éléments physiques, et vous aurez besoin d’autres éléments physiques à proximité pour les contrôler et les mesurer ; vos qubits sont stupides ; ils s’enchevêtreront avec tout ce qu’ils peuvent. Vous devez concevoir vos qubits avec le plus grand soin afin de les protéger contre toute intrusion dans l’environnement.
- Bruit : vous devez protéger vos qubits de tout type de bruit, comme les rayons cosmiques, les radiations, l’énergie thermique ou les particules parasites. Une certaine quantité de décohérence et de bruit est inévitable dans tout système physique et il est impossible de l’éliminer complètement.
- Évolutivité : Pour chaque qubit, vous devez disposer d’un ensemble de fils pour le manipuler et le mesurer. Au fur et à mesure que vous ajoutez des qubits, l’infrastructure nécessaire augmente linéairement, ce qui pose un défi technique important. Toute conception d’ordinateur quantique doit trouver un moyen d’enchevêtrer, de contrôler et de mesurer efficacement tous ces qubits au fur et à mesure qu’elle s’étend.
- Correction quantique des erreurs : La correction d’erreur quantique est un système de correction d’erreur qui permet de créer des ordinateurs quantiques tolérants aux pannes en utilisant de nombreux qubits intriqués ensemble pour représenter un qubit sans bruit. Cela nécessite un grand nombre de qubits physiques pour obtenir un qubit tolérant aux erreurs.
Implémentations physiques

Il existe une grande variété d’implémentations physiques d’ordinateurs quantiques, car il existe un grand nombre de systèmes quantiques différents à partir desquels il est possible de les construire. Voici quelques-unes des approches les plus utilisées et les plus réussies :
- Ordinateurs quantiques supraconducteurs : Les qubits supraconducteurs constituent actuellement l’approche la plus populaire. Ces qubits sont constitués de fils supraconducteurs présentant une rupture dans le supraconducteur, appelée jonction Josephson. Le type de qubit supraconducteur le plus répandu est appelé transmon.
- Ordinateurs quantiques à points quantiques : Les qubits sont constitués d’électrons ou de groupes d’électrons et le système à deux niveaux est codé dans le spin ou la charge des électrons. Ces qubits sont fabriqués à partir de semi-conducteurs tels que le silicium.
- Informatique quantique optique linéaire : Les ordinateurs quantiques optiques utilisent des photons de lumière comme qubits et opèrent sur ces qubits à l’aide d’éléments optiques tels que des miroirs, des plaques d’onde et des interféromètres.
- Ordinateurs quantiques à ions piégés : Des atomes chargés sont utilisés comme qubits, et ces atomes sont ionisés, avec un électron manquant. L’état à deux niveaux qui code le qubit correspond aux niveaux d’énergie spécifiques de l’atome, qui peuvent être manipulés ou mesurés à l’aide de micro-ondes ou de faisceaux laser.
- Ordinateurs quantiques à centre coloré ou à vide d’azote : Ces qubits sont fabriqués à partir d’atomes intégrés dans des matériaux tels que l’azote dans le diamant ou le carbure de silicium. Ils sont créés en utilisant les spins nucléaires des atomes intégrés et sont enchevêtrés avec les électrons.
- Atomes neutres dans des réseaux optiques : Cette approche permet de capturer des atomes neutres dans un réseau optique, qui est un arrangement croisé de faisceaux laser. Le système à deux niveaux pour les qubits peut être le niveau d’énergie hyperfine de l’atome ou des états excités.
Il s’agit là de quelques-unes des principales approches de la construction d’ordinateurs quantiques, chacune ayant ses propres caractéristiques et défis. L’informatique quantique évolue rapidement et le choix de la bonne approche est vital pour la réussite future.
Applications des ordinateurs quantiques

- Simulation quantique: Les ordinateurs quantiques ont le potentiel de simuler des systèmes quantiques complexes, ce qui permet d’étudier les réactions chimiques, le comportement des électrons dans les matériaux et divers paramètres physiques. Cela permet d’améliorer les panneaux solaires, les batteries, le développement de médicaments, les matériaux aérospatiaux, etc.
- Algorithmes quantiques: Des algorithmes tels que l’algorithme de Shor et l’algorithme de Grover peuvent résoudre des problèmes considérés comme insolubles pour les ordinateurs classiques. Ils trouvent des applications dans la cryptographie, l’optimisation de systèmes complexes, l’apprentissage automatique et l’IA.
- Cybersécurité: Les ordinateurs quantiques constituent une menace pour les systèmes de cryptage classiques. Toutefois, ils peuvent également contribuer à la cybersécurité grâce à la mise au point de systèmes de cryptage résistants aux quanta. La cryptographie quantique, un domaine lié à l’informatique quantique, peut renforcer la sécurité.
- Problèmes d’optimisation: Les ordinateurs quantiques peuvent résoudre des problèmes d’optimisation complexes plus efficacement que les ordinateurs classiques. Cela a des applications dans divers secteurs, de la gestion de la chaîne d’approvisionnement à la modélisation financière.
- Prévisions météorologiques et changement climatique: Bien que l’article n’en donne pas tous les détails, les ordinateurs quantiques pourraient potentiellement améliorer les modèles de prévision météorologique et aider à relever les défis liés au changement climatique. Il s’agit d’un domaine qui pourrait bénéficier de l’informatique quantique à l’avenir.
- Cryptographie quantique: La cryptographie quantique renforce la sécurité des données en utilisant les principes quantiques pour une communication sûre. À une époque où les cybermenaces sont de plus en plus nombreuses, cet aspect est crucial.
Il convient d’être prudent quant au risque de battage médiatique, car beaucoup d’affirmations sur l’utilité des ordinateurs quantiques émanent de personnes qui collectent activement des fonds pour les construire.
Mais je pense qu’historiquement, lorsqu’une nouvelle technologie est apparue, les gens de l’époque n’étaient pas les mieux placés pour savoir à quoi elle allait servir.
Par exemple, les personnes qui ont inventé les premiers ordinateurs n’ont jamais imaginé l’internet et tout ce qu’il contient. Il en sera probablement de même pour les ordinateurs quantiques.
Conclusion
Les ordinateurs quantiques s’améliorent de jour en jour et, bien que nous ne puissions pas encore les utiliser dans notre vie quotidienne, ils pourraient avoir des applications pratiques à l’avenir.
Dans cet article, j’ai abordé divers aspects des ordinateurs quantiques, notamment leurs concepts fondamentaux, tels que la superposition, l’intrication et l’interférence.
Ensuite, nous avons exploré les algorithmes quantiques, notamment l’algorithme de Shor et l’algorithme de Grover. Nous avons également approfondi la théorie de la complexité quantique et les différents modèles d’ordinateurs quantiques.
Ensuite, j’ai abordé les défis et les questions de mise en œuvre pratique associés à l’informatique quantique. Enfin, nous avons examiné le large éventail d’applications potentielles des ordinateurs quantiques.



