Ce guide complet comprend tout ce que vous, en tant que débutant, devez savoir sur la modélisation à plusieurs niveaux, une technique utilisée pour traiter des données en cluster ou groupées.
La modélisation à plusieurs niveaux, également connue sous le nom de modélisation linéaire hiérarchique, de modèles mixtes et de modélisation à effets aléatoires, trouve son utilisation dans différents domaines tels que la recherche médicale, l'économie, la sociologie, le marketing, la psychologie de l'éducation et d'autres domaines.
La modélisation à plusieurs niveaux est également utilisée dans le secteur du marketing pour l'analyse avancée des enquêtes, la modélisation de la réponse du marché et la gestion de la relation client.
Multilevel Modeling
La modélisation à plusieurs niveaux est une technique de gestion des données sous forme de cluster ou de groupe. Cette procédure peut également être utilisée pour analyser les données avec des mesures répétées. Le terme multiniveau indique des données hiérarchiques ou imbriquées, et l'analyse multiniveau signifie étudier les relations entre les variables mesurées à différents niveaux de la structure de données multiniveau.
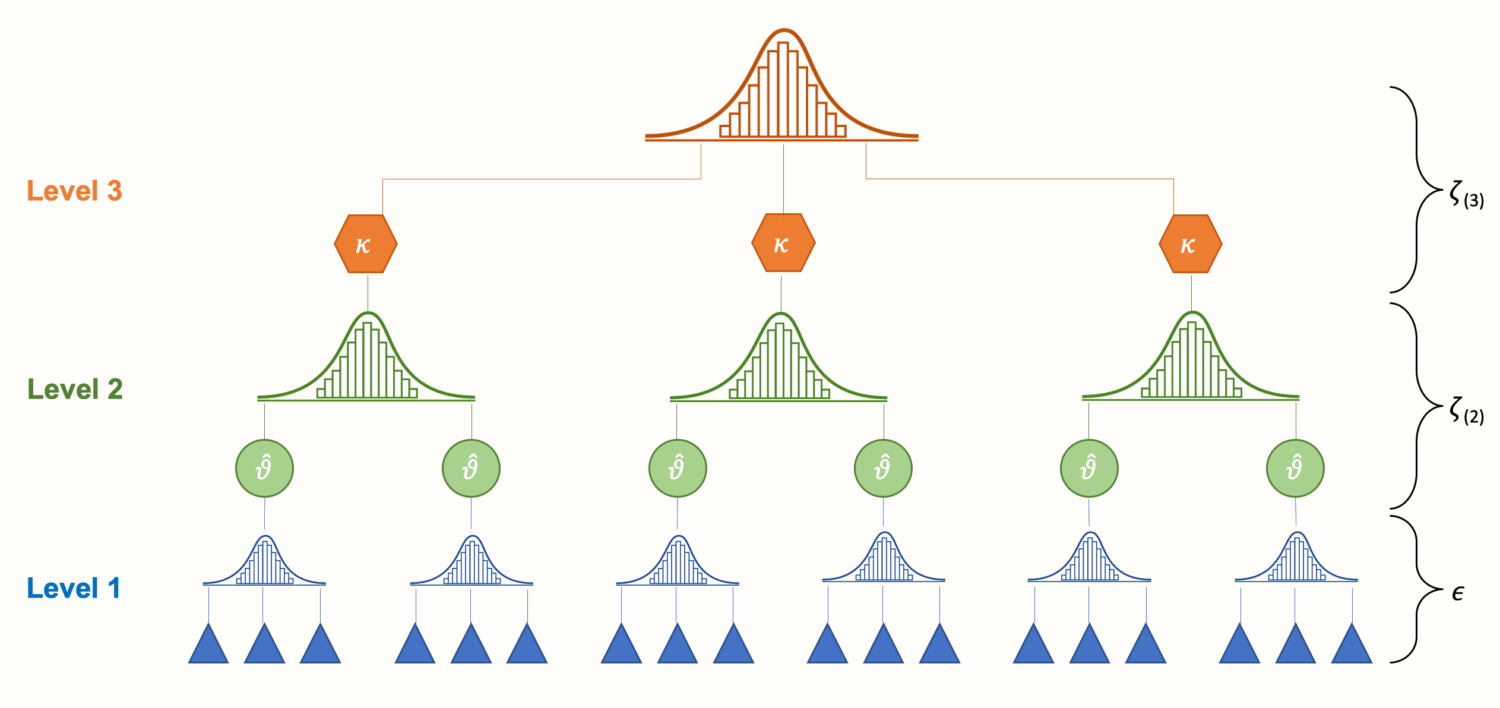
Considérons un scénario. Supposons qu'une infirmière ait été chargée d'enregistrer la tension artérielle d'un groupe de patients chaque semaine. Ils peuvent considérer les mesures successives comme un groupe à l'intérieur de chaque sujet.
Au total, la modélisation multiniveau peut traiter des données avec des périodes de mesure différentes d'un sujet à l'autre. Dans machine learning, le modèle multiniveau peut être utilisé dans des scénarios contenant des paramètres qui varient à plusieurs niveaux.
Approfondissons les concepts de modélisation à plusieurs niveaux.
Benefits of Multilevel Modeling
L'approche de modélisation à plusieurs niveaux pour modéliser la variation entre les groupes offre plusieurs avantages.
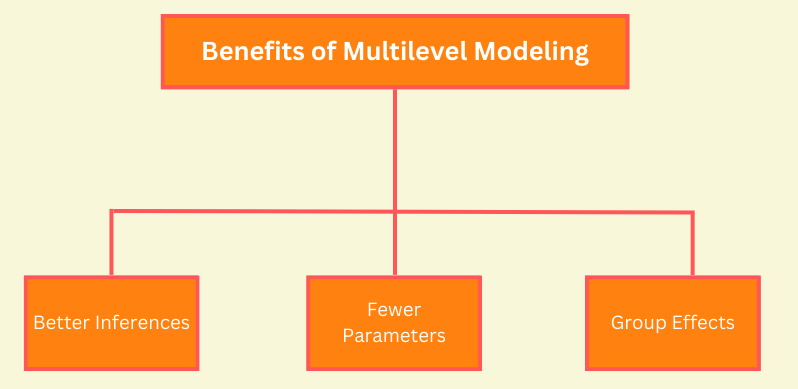
Faites de meilleures déductions
Le modèle de régression régulier ne tient pas compte de l'ensemble de la population, ce qui entraîne une sous-estimation des coefficients et une surestimation de la signification des coefficients. En revanche, la modélisation à plusieurs niveaux vous permet de faire de meilleures déductions sur la courbe de croissance des données groupées à partir desquelles l'échantillon a été sélectionné.
Moins de paramètres sont requis
Un modèle de régression régulier nécessite plusieurs variables fictives pour représenter un groupe de données complexe. En revanche, la modélisation à plusieurs niveaux nécessite des périmètres moindres pour la même chose.
Effets de groupe
Les modèles multiniveaux permettent le partage d'informations entre les groupes en supposant que les effets aléatoires sont dérivés d'une distribution commune. Ceci, contrairement à la régression régulière, améliore considérablement la précision de la prédiction pour les groupes avec moins de données.
Types of Multilevel Modeling
Passons à autre chose, discutons des différents types de modèles multiniveaux.
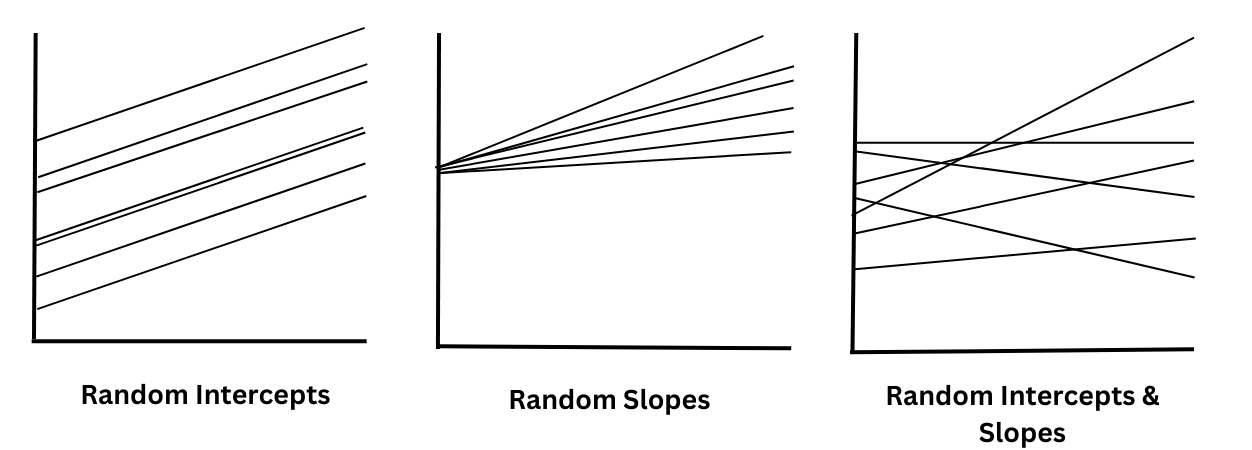
# 1. Modèle d'interceptions aléatoires
Dans le modèle d'interceptions aléatoires, le terme d'interception peut varier d'un cluster à l'autre. Une variable aléatoire doit être ajoutée pour représenter le terme d'interception qui aide à prédire les scores de la variable dépendante pour chaque observation.
Ce modèle suppose que les pentes restent constantes dans différents contextes et donne des informations sur les corrélations intraclasses, qui jouent un rôle central pour déterminer si le modèle multiniveau doit réellement être mis en œuvre ou non.
# 2. Modèle de pentes aléatoires
Dans le modèle à pentes aléatoires, les pentes fluctuent par rapport à la matrice de corrélation et, par conséquent, les pentes ont tendance à différer selon les variables de regroupement telles que le temps ou les individus.
Ici aussi, les interceptions restent fixes dans différents contextes. Le modèle de pente aléatoire ou le modèle de coefficient aide à comprendre la variabilité entre les groupes, ce qui n'est pas possible de déterminer par le modèle d'interception aléatoire seul.
# 3. Modèle d'interceptions et de pentes aléatoires
Dans ce modèle, comme son nom l'indique, les interceptions et les pentes peuvent varier d'un groupe à l'autre. Cela signifie que leur valeur ne cesse de changer dans différents contextes. Le modèle d'interceptions et de pentes aléatoires est considéré comme le type de modèle le plus réaliste.
How does Multilevel Modelling work?
Les modèles multiniveaux sont un type de modèle statistique qui prend en compte plusieurs niveaux de variation. Ces modèles sont également appelés modèles linéaires hiérarchiques, modèles linéaires à effets mixtes, modèles mixtes, imbriqués. modèles de données, des coefficients aléatoires, des modèles à effets aléatoires, des modèles à paramètres aléatoires ou des plans en parcelles divisées.
Différents types de données recueillies à partir d'observations faites au cours de la recherche humaine et des sciences biologiques décrivent une structure hiérarchique ou en cluster.
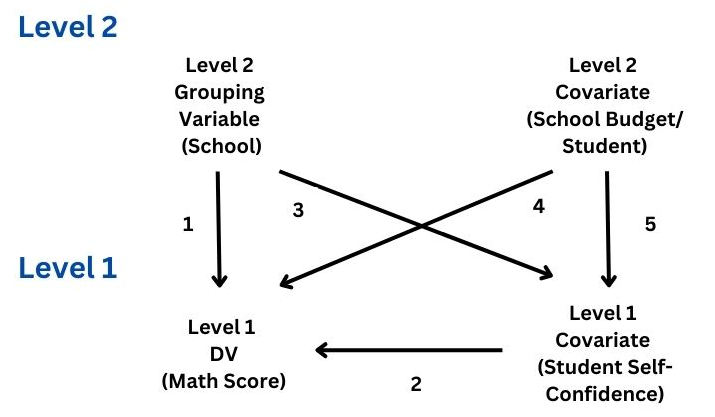
Par exemple, les enfants ayant les mêmes parents biologiques possèdent plus de caractéristiques physiques et mentales similaires que des individus choisis au hasard dans une population plus large.
De même, les employés ou les étudiants peuvent être séparés en fonction de facteurs individuels tels que l'emplacement. Les actions individuelles liées progressivement se traduisent également par des structures de données à plusieurs niveaux.
Les modèles multiniveaux considèrent les éléments résiduels à chaque niveau de la structure hiérarchique pour aboutir à la formation d'une structure de données hiérarchique.
Les modèles en couches aident également les autorités scolaires à organiser les résultats des élèves, ce qui inclut généralement les résidus pour les niveaux de l'école et des élèves.
Pour les non-initiés, les résidus scolaires, ou effets liés à l'école, sont un ensemble de caractéristiques scolaires non observées qui peuvent influer sur les résultats des élèves. Ces effets peuvent déclencher la relation entre les résultats des élèves. Par conséquent, il devient prudent de diviser la variance des résidus en deux parties : une composante inter-écoles et une composante intra-écoles.
When should you use Multilevel Modeling?
Voici quelques raisons pour lesquelles vous devriez préférer utiliser des modèles à plusieurs niveaux :
Faire des déductions correctes
Dans les méthodes standard de régression multiple, l'unité d'analyse est considérée comme une observation indépendante.
L'incompétence de la régression multiple pour reconnaître les structures hiérarchiques entraîne une sous-estimation des erreurs normales, conduisant à une surestimation de la signification statistique. L'omission du regroupement affecte largement la précision des prédictions pour les variables prédictives de haut niveau.
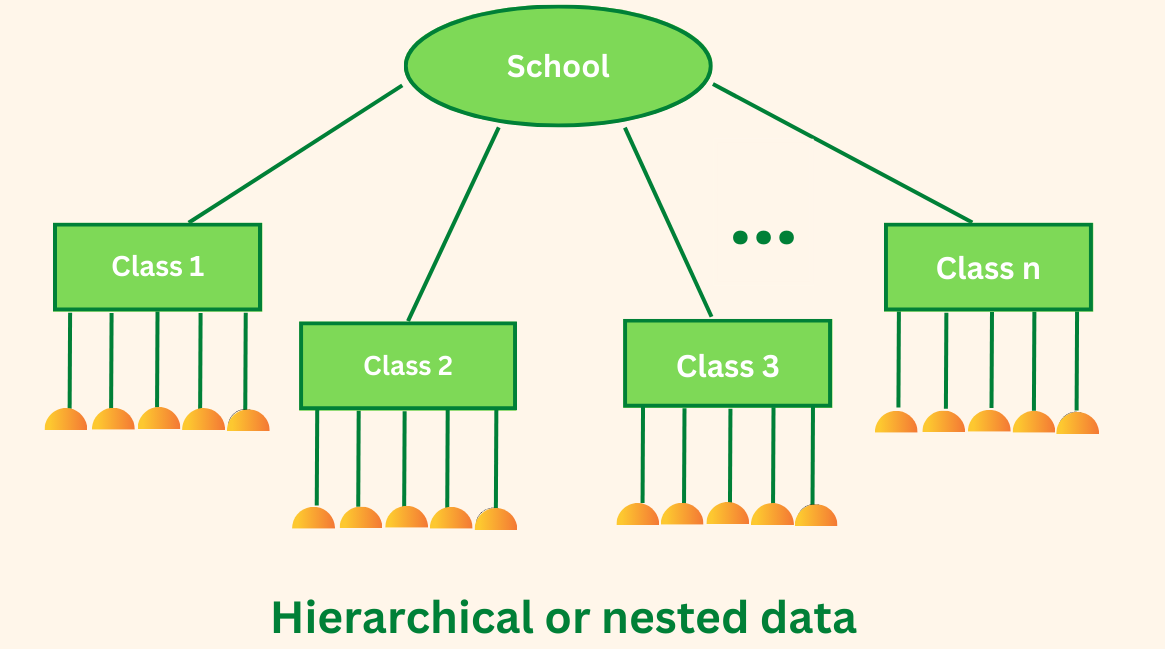
Inférence à une population de groupes
Le modèle à plusieurs niveaux traite les groupes de l'échantillon comme un échantillon aléatoire choisi dans un groupe, qui sert de domaine de recherche important dans plusieurs cas. Cela ne peut pas être accompli par le modèle à effets fixes, où il est impossible de faire des inférences au-delà des groupes de l'échantillon.
Évaluation des effets de groupe
La modélisation à plusieurs niveaux est la meilleure méthode pour déterminer les effets distincts sur les observations et les caractéristiques non observées du groupe.
Intérêt substantiel pour les effets de groupe
Dans plusieurs domaines de recherche, une question clé concerne l'étendue du regroupement dans les résultats individuels et la détermination de son existence dans les groupes « périphériques ».
Par exemple, dans les évaluations des performances des écoles, l'accent est mis sur l'identification des effets « à valeur ajoutée » liés à l'école sur les performances des élèves. Cela peut être déterminé par un modèle à plusieurs niveaux après avoir ajusté les réalisations antérieures.
Learning Resources
Voici les meilleurs supports d'apprentissage auxquels vous pouvez vous référer pour comprendre les concepts de la modélisation à plusieurs niveaux.
# 1. Modélisation multiniveaux en langage clair
La modélisation multiniveaux en langage clair de Karen Robson et David Pavalin est l'un des meilleurs livres sur la modélisation multiniveaux car il présente les phases complètes d'une analyse multiniveaux pour les étudiants et les instructeurs.
| Aperçu | Produit | Rating | Prix | |
|---|---|---|---|---|
|
Modélisation multiniveaux en langage clair | $32.22 | Acheter sur Amazon |
"L'approche simple" du livre aide le lecteur à saisir l'idée derrière le sujet plutôt que d'expliquer la formule trouvée dans d'autres supports d'apprentissage. De même, les éducateurs pourront rattraper très rapidement la voie avancée de l'analyse à plusieurs niveaux.
# 2. Analyse multiniveau : introduction à la modélisation multiniveau
Rédigé par TAB Snijders, Multilevel Analysis: An Introduction To Basic And Advanced Multilevel Modeling fournit un contenu accessible sur l'analyse multiniveau adapté pour répondre aux exigences des chercheurs avancés et des enseignants souhaitant mener des recherches dans le même domaine.
| Aperçu | Produit | Rating | Prix | |
|---|---|---|---|---|
|
Analyse multiniveau : introduction à la modélisation multiniveau de base et avancée | $48.15 | Acheter sur Amazon |
En dehors de cela, les lecteurs qui cherchent à approfondir leurs connaissances dans le domaine de l'analyse multiniveau trouveront dans le livre une ressource idéale.
Le livre comprend les différentes méthodes, techniques et problèmes liés à la modélisation et à l'analyse à plusieurs niveaux et offre aux lecteurs une compréhension claire, conceptuelle et pratique des études à plusieurs niveaux.
# 3. Modélisation à plusieurs niveaux à l'aide de R
Modélisation à plusieurs niveaux à l'aide de R par W. Holmes Finch, Jocelyn E. Bolin et Ken Kelley est un guide précieux sur la modélisation de données à plusieurs niveaux à l'aide de l'environnement logiciel R. Le livre passe en revue et présente les bases des modèles multiniveaux et explique comment implémenter ces modèles à l'aide de R.
| Aperçu | Produit | Rating | Prix | |
|---|---|---|---|---|
|
Modélisation multiniveaux à l'aide de R (Chapman & Hall/CRC Statistics in the Social and Behavioral Sciences) | $61.64 | Acheter sur Amazon |
Il démontre également le processus d'utilisation de la modélisation à plusieurs niveaux avec des données longitudinales. En dehors de cela, vous trouverez également les modèles pour les variables dépendantes catégorielles dans les données à un niveau et à plusieurs niveaux.
Récapitulation
Ici, nous avons couvert les concepts de base de la modélisation à plusieurs niveaux, de ses avantages au fonctionnement de la technique. Si vous êtes un étudiant ou un enseignant, les supports d'apprentissage mentionnés ci-dessus vous offriront une aide précieuse pour comprendre les concepts avancés de la modélisation multiniveaux.
Vous pouvez également explorer certains top modèles d'apprentissage automatique.
