Dans ce tutoriel, vous apprendrez à multiplier deux matrices en Python.
Vous commencerez par apprendre les conditions d’une multiplication matricielle valide et écrirez une fonction Python personnalisée pour multiplier des matrices. Ensuite, vous verrez comment vous pouvez obtenir le même résultat en utilisant des compréhensions de listes imbriquées.
Enfin, vous utiliserez NumPy et ses fonctions intégrées pour effectuer une multiplication matricielle plus efficacement.
Comment vérifier que la multiplication matricielle est valide ?
Avant d’écrire du code Python pour la multiplication matricielle, revisitons les bases de la multiplication matricielle.
La multiplication matricielle entre deux matrices A et B n’est valide que si le nombre de colonnes de la matrice A est égal au nombre de lignes de la matrice B.
Vous avez probablement déjà rencontré cette condition de multiplication matricielle. Mais vous êtes-vous déjà demandé pourquoi ?
Eh bien, c’est à cause de la façon dont fonctionne la multiplication matricielle. Regardez l’image ci-dessous.
Dans notre exemple générique, la matrice A a m lignes et n colonnes. Et la matrice B a n lignes et p colonnes.

Quelle est la forme de la matrice produit ?
L’élément à l’indice (i, j) dans la matrice résultante C est le produit par points de la ligne i de la matrice A et de la colonne j de la matrice B.
Ainsi, pour obtenir un élément à un indice particulier dans la matrice résultante C, vous devrez calculer le produit point de la ligne et de la colonne correspondantes dans les matrices A et B, respectivement.
En répétant le processus ci-dessus, vous obtiendrez la matrice produit C de forme m x p – avec m lignes et p colonnes, comme indiqué ci-dessous.

Le produit de points ou le produit intérieur entre deux vecteurs a et b est donné par l’équation suivante.

Résumons maintenant :
- Il est évident que le produit point n’est défini qu’entre des vecteurs de même longueur.
- Ainsi, pour que le produit point entre une ligne et une colonne soit valide – lors de la multiplication de deux matrices – il faut que les deux aient le même nombre d’éléments.
- Dans l’exemple générique ci-dessus, chaque ligne de la matrice A a n éléments. Et chaque colonne de la matrice B a également n éléments.
Si vous y regardez de plus près, n est le nombre de colonnes de la matrice A, et c’est aussi le nombre de lignes de la matrice B. C’est précisément la raison pour laquelle le nombre de colonnes de la matrice A doit être égal au nombre de lignes de la matrice B.
J’espère que vous avez compris la condition de validité de la multiplication matricielle et la manière d’obtenir chaque élément de la matrice produit.
Nous allons maintenant écrire du code Python pour multiplier deux matrices.
Écrire une fonction Python personnalisée pour multiplier des matrices
Dans un premier temps, écrivons une fonction personnalisée pour multiplier des matrices.
Cette fonction doit effectuer les opérations suivantes :
- Accepter deux matrices, A et B, comme entrées.
- Vérifier si la multiplication matricielle entre A et B est valide.
- Si elle est valide, elle multiplie les deux matrices A et B et renvoie la matrice produit C.
- Dans le cas contraire, renvoyez un message d’erreur indiquant que les matrices A et B ne peuvent pas être multipliées.
Étape 1: Générez deux matrices d’entiers à l’aide de la fonction random.randint() de NumPy. Vous pouvez également déclarer les matrices comme des listes Python imbriquées.
import numpy as np
np.random.seed(27)
A = np.random.randint(1,10,size = (3,3))
B = np.random.randint(1,10,size = (3,2))
print(f "Matrice A:\n {A}\n")
print(f "Matrice B:\n {B}\n")
# Sortie
Matrice A :
[[4 9 9]
[9 1 6]
[9 2 3]]
Matrice B :
[[2 2]
[5 7]
[4 4]]Étape 2 : Définissez la fonction multiply_matrix(A,B). Cette fonction prend deux matrices A et B en entrée et renvoie la matrice produit C si la multiplication de la matrice est valide.
def multiplier_matrix(A,B) :
global C
si A.shape<x><x><x>[1]</x></x></x> == B.shape<x><x><x>[0]</x></x></x>:
C = np.zeros((A.shape<x><x><x>[0]</x></x></x>,B.shape<x><x><x>[1]</x></x></x>),dtype = int)
for row in range(rows) :
for col in range(cols) :
for elt in range(len(B)) :
C[ligne, col] = A[ligne, elt] * B[elt, col]
retour C
sinon :
return "Désolé, je ne peux pas multiplier A et B"Analyse de la définition de la fonction
Procédons à l’analyse de la définition de la fonction.
Déclarez C comme une variable globale: Par défaut, toutes les variables à l’intérieur d’une fonction Python ont une portée locale. Vous ne pouvez pas y accéder depuis l’extérieur de la fonction. Pour que la matrice produit C soit accessible de l’extérieur, nous devons la déclarer comme variable globale. Il suffit d’ajouter le qualificatif global avant le nom de la variable.
Vérifiez que la multiplication de la matrice est valide : Utilisez l’attribut shape pour vérifier si A et B peuvent être multipliés. Pour tout tableau arr, arr.shape<x><x><x>[0]</x></x></x> et arr.shape<x><x><x>[1]</x></x></x> indiquent respectivement le nombre de lignes et de colonnes. Ainsi, si A.shape<x><x><x>[1]</x></x></x> == B.shape<x><x><x>[0]</x></x></x>, la multiplication de la matrice est valide. Ce n’est que si cette condition est vraie que la matrice du produit sera calculée. Dans le cas contraire, la fonction renvoie un message d’erreur.
Utilisez des boucles imbriquées pour calculer les valeurs : Pour calculer les éléments de la matrice résultante, nous devons parcourir les lignes de la matrice A, ce que fait la boucle for externe. La boucle for interne nous aide à parcourir les colonnes de la matrice B. Et la boucle for la plus interne permet d’accéder à chaque élément de la colonne sélectionnée.
▶️ Maintenant que nous avons appris comment fonctionne la fonction Python de multiplication des matrices, appelons la fonction avec les matrices A et B que nous avons générées plus tôt.
multiplier_matrix(A,B)
# Sortie
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])La multiplication matricielle entre A et B étant valide, la fonction multiply_matrix() renvoie la matrice produit C.
Utiliser la compréhension des listes imbriquées de Python pour multiplier des matrices
Dans la section précédente, vous avez écrit une fonction Python pour multiplier des matrices. Vous allez maintenant voir comment vous pouvez utiliser la compréhension des listes imbriquées pour faire la même chose.
Voici la compréhension de liste imbriquée pour multiplier des matrices.
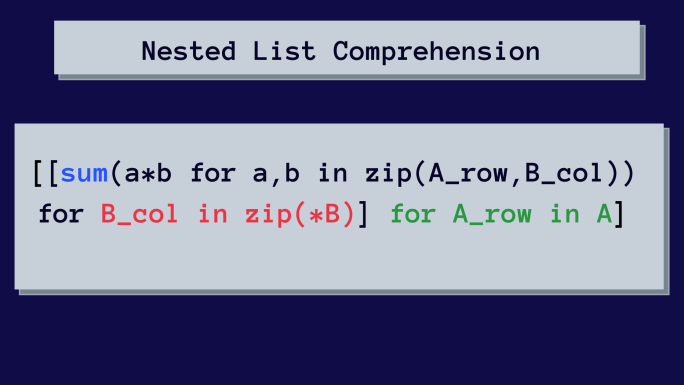
À première vue, cela peut sembler compliqué. Mais nous allons analyser la compréhension de liste imbriquée étape par étape.
Concentrons-nous sur une compréhension de liste à la fois et identifions ce qu’elle fait.
Nous utiliserons le modèle général suivant pour la compréhension de liste :
[<do-this> for <item> in <iterable>]
où,
<do-this> : ce que vous souhaitez faire - expression ou opération
<item> : chaque élément sur lequel vous souhaitez effectuer l'opération
<iterable> : l'itérable (liste, tuple, etc.) que vous parcourez en boucle▶️ Consultez notre guide List Comprehension in Python – with Examples pour approfondir votre compréhension.
Avant de poursuivre, veuillez noter que nous souhaitons construire la matrice résultante C une ligne à la fois.
La compréhension des listes imbriquées expliquée
Étape 1 : Calculer une valeur unique dans la matrice C
Étant donné la ligne i de la matrice A et la colonne j de la matrice B, l’expression ci-dessous donne l’entrée à l’indice (i, j) dans la matrice C.
sum(a*b for a,b in zip(A_row, B_col)
# zip(A_row, B_col) renvoie un itérateur de tuples
# Si A_row = [a1, a2, a3] & B_col = [b1, b2, b3]
# zip(A_row, B_col) renvoie (a1, b1), (a2, b2), et ainsi de suiteSi i= j = 1, l’expression renverra l’entrée c_11 de la matrice C. Vous pouvez donc obtenir un élément dans une ligne de cette manière.
Étape 2 : Construire une ligne dans la matrice C
Notre prochain objectif est de construire une ligne entière.
Pour la ligne 1 de la matrice A, vous devez passer par toutes les colonnes de la matrice B pour obtenir une ligne complète dans la matrice C.
Revenez au modèle de compréhension de liste.
- Remplacez
<do-this>par l’expression de l’étape 1, car c’est ce que vous voulez faire. - Ensuite, remplacez
<item>parB_col - chaquecolonne de la matrice B. - Enfin, remplacez
<iterable>parzip(*B)-la liste contenant toutes les colonnes de la matrice B.
Et voici la première compréhension de la liste.
[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
# zip(*B) : * est l'opérateur de décompression
# zip(*B) renvoie une liste de colonnes de la matrice BEtape 3 : Construire toutes les lignes et obtenir la matrice C
Ensuite, vous devrez remplir la matrice produit C en calculant le reste des lignes.
Pour ce faire, vous devez parcourir en boucle toutes les lignes de la matrice A.
Revenez encore une fois à la compréhension de la liste et faites ce qui suit.
- Remplacez
<do-this>par la liste de compréhension de l’étape 2. Rappelez-vous que nous avons calculé une ligne entière à l’étape précédente. - Maintenant, remplacez
<item>parA_row - chaqueligne de la matrice A. - Et votre
<iterable>est la matrice A elle-même, puisque vous parcourez ses lignes en boucle.
Et voici notre compréhension finale de la liste imbriquée 🎊
[[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
pour A_row dans A]Il est temps de vérifier le résultat ! ✔
# convertir en <a href="https://geekflare.com/fr/numpy-reshape-arrays-in-python/">tableau NumPy</a> en utilisant np.array()
C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]]
pour A_row dans A])
# Sortie :
[[ 89 107]
[ 47 49]
[ 40 44]]Si vous y regardez de plus près, vous constaterez qu’il s’agit de l’équivalent des boucles for imbriquées que nous avons eues plus tôt, mais qu’elles sont plus succinctes.
Vous pouvez également faire cela de manière encore plus efficace en utilisant certaines fonctions intégrées. Nous allons les découvrir dans la section suivante.
Utilisez NumPy matmul() pour multiplier des matrices en Python
La fonction np.matmul() prend deux matrices en entrée et renvoie le produit si la multiplication matricielle entre les matrices en entrée est valide.
C = np.matmul(A,B)
print(C)
# Sortie :
[[ 89 107]
[ 47 49]
[ 40 44]]Remarquez que cette méthode est plus simple que les deux méthodes que nous avons apprises plus tôt. En fait, au lieu de np.matmul(), vous pouvez utiliser un opérateur @ équivalent, et nous allons le voir tout de suite.
Comment utiliser l’opérateur @ en Python pour multiplier des matrices
En Python, @ est un opérateur binaire utilisé pour la multiplication de matrices.
Il opère sur deux matrices, et en général, sur des tableaux NumPy à N dimensions, et renvoie la matrice produit.
Remarque : vous devez disposer de Python 3.5 ou d’une version ultérieure pour utiliser l’opérateur
@.
Voici comment vous pouvez l’utiliser.
C = A@B
print(C)
# Sortie
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])Remarquez que la matrice produit C est la même que celle que nous avons obtenue précédemment.
Pouvez-vous utiliser np.dot() pour multiplier des matrices ?
Si vous avez déjà rencontré un code qui utilise np.dot() pour multiplier deux matrices, voici comment cela fonctionne.
C = np.dot(A,B)
print(C)
# Sortie :
[[ 89 107]
[ 47 49]
[ 40 44]]Vous verrez que np.dot(A, B) renvoie également le produit matriciel attendu.
Cependant, selon la documentation NumPy, vous ne devez utiliser np.dot() que pour calculer le produit point de deux vecteurs unidimensionnels et non pour la multiplication matricielle.
Rappelez-vous de la section précédente, l’élément à l’index (i, j) de la matrice produit C est le produit point de la ligne i de la matrice A, et de la colonne j de la matrice B.
Comme NumPy diffuse implicitement cette opération de produit point à toutes les lignes et à toutes les colonnes, vous obtenez la matrice produit résultante. Mais pour garder votre code lisible et éviter toute ambiguïté, utilisez plutôt np.matmul() ou l’opérateur @.
Conclusion
🎯 Dans ce tutoriel, vous avez appris ce qui suit.
- Condition de validité de la multiplication matricielle : nombre de colonnes de la matrice A = nombre de lignes de la matrice B.
- Comment écrire une fonction Python personnalisée qui vérifie si la multiplication matricielle est valide et renvoie la matrice produit. Le corps de la fonction utilise des boucles for imbriquées.
- Ensuite, vous avez appris à utiliser des compréhensions de listes imbriquées pour multiplier des matrices. Elles sont plus succinctes que les boucles for mais sont sujettes à des problèmes de lisibilité.
- Enfin, vous avez appris à utiliser la fonction intégrée de NumPy np.matmul() pour multiplier les matrices et comment cette méthode est la plus efficace en termes de vitesse.
- Vous avez également appris à utiliser l’opérateur @ pour multiplier deux matrices en Python.
Voilà qui conclut notre discussion sur la multiplication matricielle en Python. Dans une prochaine étape, apprenez à vérifier si un nombre est premier en Python. Ou encore, résolvez des problèmes intéressants sur les chaînes de caractères en Python.
Bon apprentissage!🎉

