Le tri est l’une des fonctions les plus utilisées en programmation. Et il faudra du temps pour effectuer le tri si nous n’utilisons pas le bon algorithme.
Dans cet article, nous allons discuter des différents algorithmes de tri.
Nous vous guiderons à travers les différents algorithmes de tri avec chaque étape de leur mise en œuvre. L’implémentation se fera en Python. Vous pouvez facilement le convertir dans n’importe quel langage une fois que vous avez compris l’algorithme. C’est la question de la syntaxe du langage.
Nous verrons différents algorithmes du pire au meilleur dans ce tutoriel. Ne vous inquiétez donc pas. Suivez l’article et mettez-les en œuvre.
Plongeons dans les algorithmes de tri.
Tri par insertion
Le tri par insertion est l’un des algorithmes de tri les plus simples. Il est facile à mettre en œuvre. Il vous coûtera plus de temps pour trier un tableau. Il ne sera pas utilisé dans la plupart des cas pour trier des tableaux plus grands.
L’algorithme de tri par insertion conserve des sous-parties triées et non triées dans le tableau donné.
La sous-partie triée ne contient que le premier élément au début du processus de tri. Nous allons prendre un élément du tableau non trié et le placer à la bonne position dans le sous-réseau trié.
Voyons les illustrations visuelles du tri par insertion étape par étape à l’aide d’un exemple.
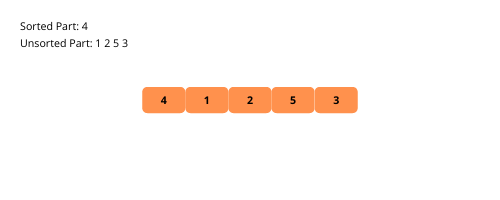
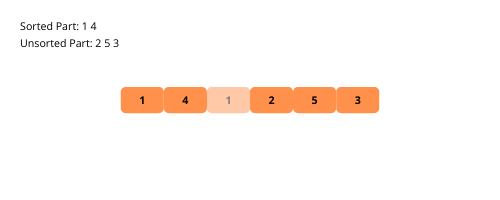
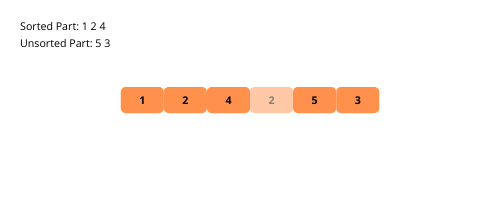
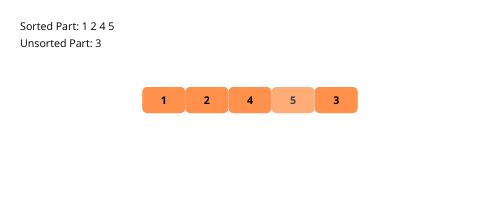
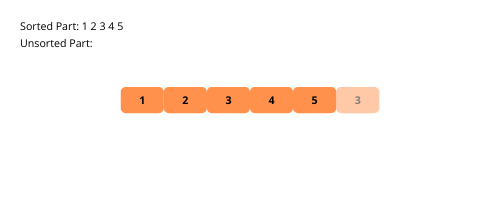
Voyons les étapes de la mise en œuvre du tri par insertion.
- Initialisez le tableau avec des données fictives (entiers).
- Itérer sur le tableau donné à partir du deuxième élément.
- Prenez la position actuelle et l’élément dans deux variables.
- Écrivez une boucle qui itère jusqu’au premier élément du tableau ou jusqu’à ce qu’apparaisse l’élément inférieur à l’élément actuel.
- Mettre à jour l’élément actuel avec l’élément précédent.
- Décrémentation de la position actuelle.
- Ici, la boucle doit atteindre le début du tableau ou trouver un élément plus petit que l’élément courant. Remplacer l’élément de la position actuelle par l’élément actuel.
La complexité temporelle du tri par insertion est O(n^2), et la complexité spatiale est O(1).
Voilà, nous avons trié le tableau donné. Exécutons le code suivant. J’espère que vous avez installé Python. Si ce n’est pas le cas, consultez le guide d’installation. Vous pouvez également utiliser un compilateur Python en ligne.
def insertion_sort(arr, n) :
for i in range(1, n) :
## position et élément actuels
position_actuelle = i
élément_actuel = arr<x><x><x><x><x>[i]</x></x></x></x></x>
## itération jusqu'à ce que
### qu'il atteigne le premier élément ou
### l'élément actuel est plus petit que l'élément précédent
while position_actuelle > 0 et élément_actuel <
arr[position_actuelle - 1] :
## mise à jour de l'élément actuel avec l'élément précédent
arr<x>[position_actuelle]</x> = arr[position_actuelle - 1]
## déplacement vers la position précédente
position_actuelle -= 1
## mise à jour de l'élément de la position actuelle
arr<x>[position_actuelle]</x> = élément_actuel
if __name__ == '__main__' :
## initialisation du tableau
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
insertion_sort(arr, 9)
## impression du tableau
print(str(arr))Tri de sélection
Le tri par sélection est similaire au tri par insertion avec une légère différence. Cet algorithme divise également le tableau en sous-parties triées et non triées. Ensuite, à chaque itération, nous prenons l’élément minimum de la sous-partie non triée et le plaçons en dernière position de la sous-partie triée.
Illustrons le tri par sélection pour une meilleure compréhension.
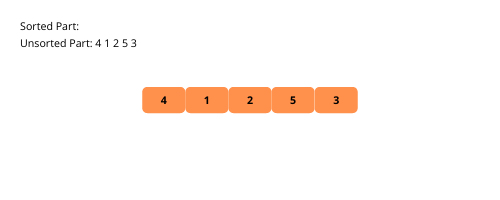
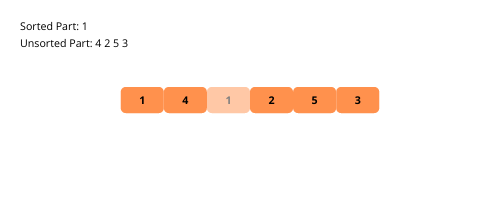
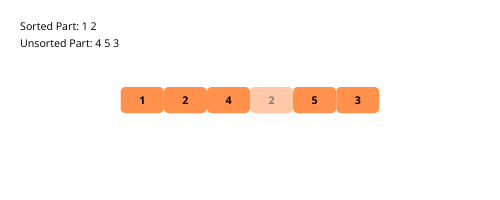
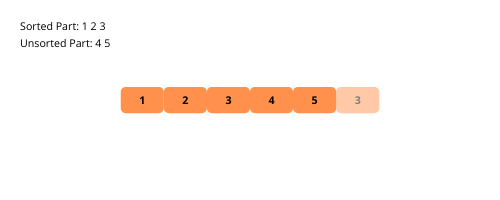
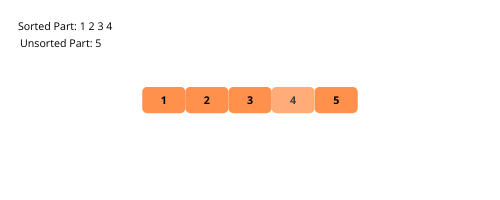
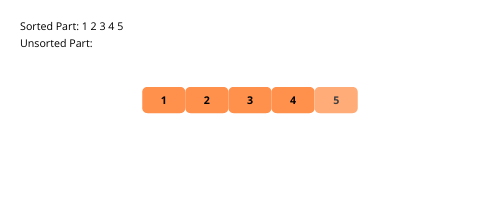
Voyons les étapes de la mise en œuvre du tri par sélection.
- Initialisez le tableau avec des données fictives (entiers).
- Interrogez le tableau donné.
- Conservez l’indice de l’élément minimum.
- Ecrivez une boucle qui itère de l’élément courant au dernier élément.
- Vérifiez si l’élément courant est inférieur à l’élément minimum ou non.
- Si l’élément courant est inférieur à l’élément minimum, remplacez l’index.
- Nous disposons de l’indice de l’élément minimal. Remplacez l’élément actuel par l’élément minimum à l’aide des indices.
La complexité en temps du tri par sélection est O(n^2), et la complexité en espace est O(1).
Essayez d’implémenter l’algorithme car il est similaire au tri par insertion. Vous pouvez voir le code ci-dessous.
def selection_sort(arr, n) :
for i in range(n) :
## pour stocker l'indice de l'élément minimum
min_element_index = i
for j in range(i 1, n) :
## vérification et remplacement de l'indice de l'élément minimum
si arr<x><x><x><x><x>[j]</x></x></x></x></x> < arr<x><x>[min_element_index]</x></x>:
min_element_index = j
## remplacement de l'élément courant par l'élément minimum
arr<x><x><x><x><x>[i]</x></x></x></x></x>, arr<x><x>[min_element_index]</x></x> = arr<x><x>[min_element_index]</x></x>, arr<x><x><x><x><x>[i]</x></x></x></x></x>
if __name__ == '__main__' :
## Initialisation du tableau
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
selection_sort(arr, 9)
## impression du tableau
print(str(arr))Tri à bulles
Le tri à bulles est un algorithme simple. Il permute les éléments adjacents à chaque itération jusqu’à ce que le tableau soit trié.
Il itère sur le tableau et déplace l’élément courant à la position suivante jusqu’à ce qu’il soit inférieur à l’élément suivant.
Les illustrations nous aident à comprendre visuellement le tri à bulles . Voyons-les.
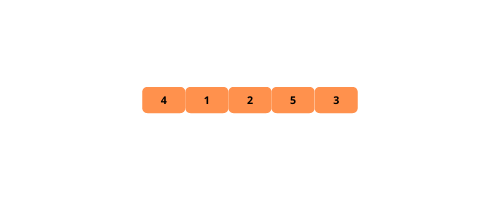
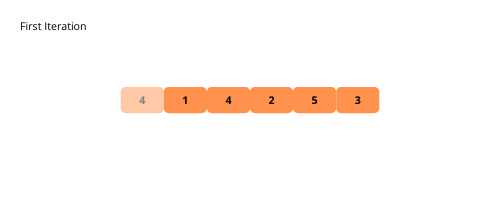
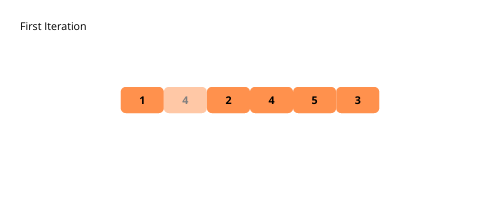
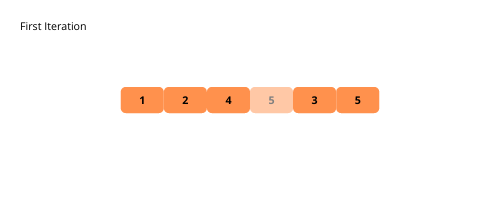
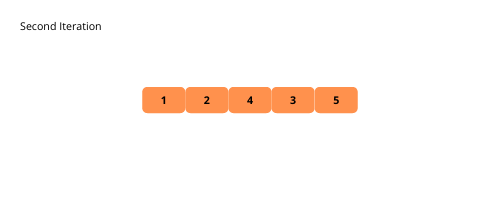
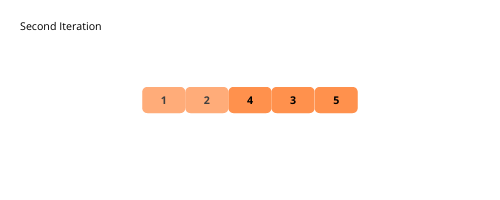
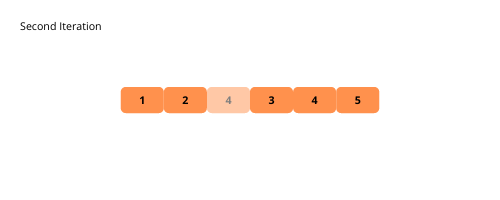
Voyons les étapes de la mise en œuvre du tri à bulles.
- Initialisez le tableau avec des données fictives (entiers).
- Interrogez le tableau donné.
- Itérer de 0 à n-i-1. Les i derniers éléments sont déjà triés.
- Vérifiez si l’élément courant est plus grand que l’élément suivant ou non.
- Si l’élément courant est plus grand que l’élément suivant, échangez les deux éléments.
- Itérer de 0 à n-i-1. Les i derniers éléments sont déjà triés.
La complexité temporelle du tri à bulles est O(n^2), et la complexité spatiale est O(1).
Vous pouvez facilement mettre en œuvre le tri à bulles. Voyons le code.
def bubble_sort(arr, n) :
for i in range(n) :
## itère de 0 à n-i-1 car les i derniers éléments sont déjà triés
for j in range(n - i - 1) :
## vérification de l'élément suivant
if arr<x><x><x><x><x>[j]</x></x></x></x></x> > arr[j 1] :
## échanger les éléments adjacents
arr<x><x><x><x><x>[j]</x></x></x></x></x>, arr[j 1] = arr[j 1], arr<x><x><x><x><x>[j</x></x></x></x></x>]
if __name__ == '__main__' :
## initialisation du tableau
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
bubble_sort(arr, 9)
## impression du tableau
print(str(arr))Fusionner les tris
Le tri par fusion est un algorithme récursif qui permet de trier un tableau donné. Il est plus efficace que les algorithmes précédents en termes de complexité temporelle. Il suit l’approche “diviser pour mieux régner”.
L’algorithme de tri par fusion divise le tableau en deux moitiés et les trie séparément. Après avoir trié les deux moitiés du tableau, il les fusionne en un seul tableau trié.
Comme il s’agit d’un algorithme récursif, il divise le tableau jusqu’à ce qu’il devienne le plus simple (tableau à un seul élément) à trier.
Il est temps de passer à l’illustration. Voyons ce qu’il en est.
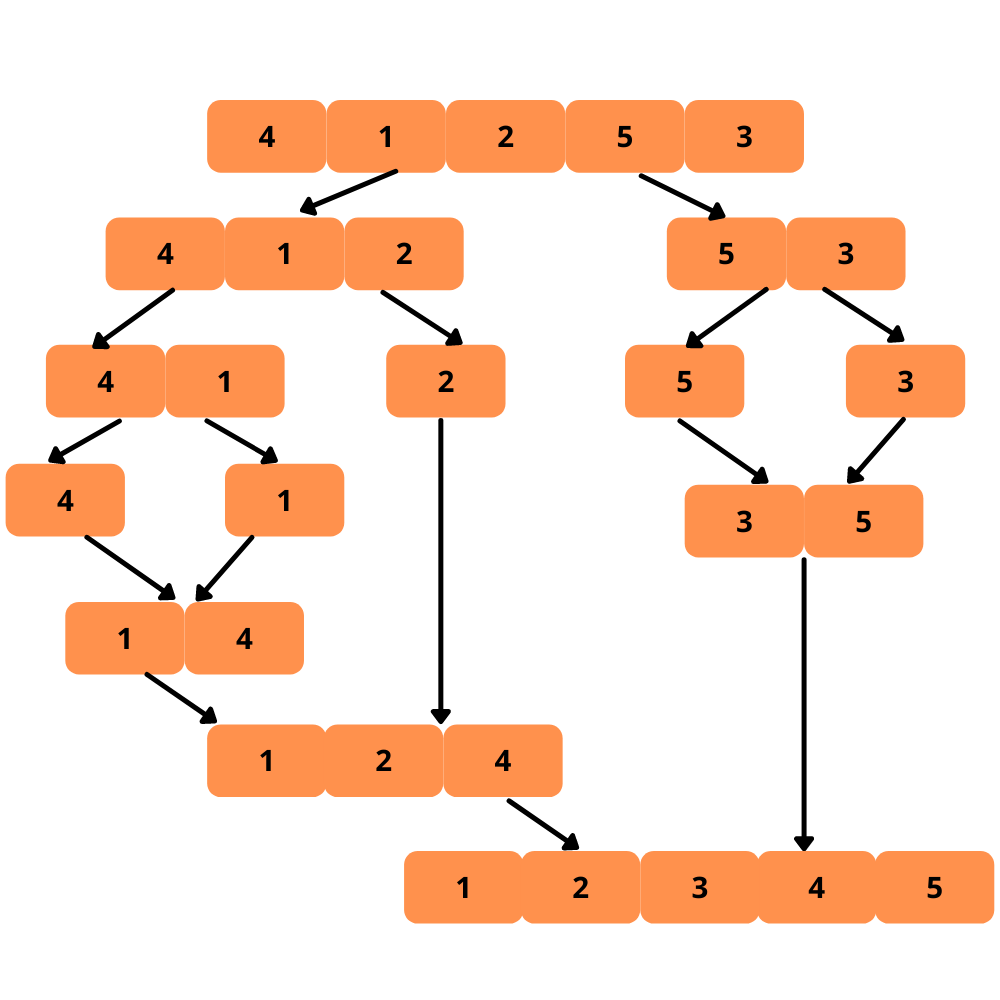
Voyons les étapes de la mise en œuvre du tri par fusion.
- Initialisez le tableau avec des données fictives (entiers).
- Écrivez une fonction appelée merge pour fusionner les sous-réseaux en un seul tableau trié. Elle accepte les arguments tableau, index gauche, moyen et droit.
- Obtenez les longueurs des sous-réseaux gauche et droit en utilisant les indices donnés.
- Copiez les éléments du tableau dans les tableaux de gauche et de droite respectifs.
- Itérer sur les deux sous-ensembles.
- Comparez les éléments des deux sous-réseaux.
- Remplacez l’élément du tableau par le plus petit élément des deux sous-ensembles pour le tri.
- Vérifiez s’il reste des éléments dans les deux sous-ensembles.
- Ajoutez-les au tableau.
- Écrivez une fonction appelée merge_sort avec comme paramètres le tableau et les index gauche et droit.
- Si l’indice gauche est supérieur ou égal à l’indice droit, la fonction retourne.
- Trouvez le point central du tableau pour le diviser en deux moitiés.
- Appelez récursivement merge_sort en utilisant les index gauche, droit et moyen.
- Après les appels récursifs, fusionnez le tableau avec la fonction merge .
La complexité temporelle du tri par fusion est O(nlogn), et la complexité spatiale est O(1).
C’est tout pour l’implémentation de l’algorithme de tri par fusion. Consultez le code ci-dessous.
def merge(arr, left_index, mid_index, right_index) :
## tableaux gauche et droit
tableau_gauche = arr[indice_gauche:indice_milieu 1]
tableau_droit = arr[indice_milieu 1:indice_droit 1]
## obtenir les longueurs des tableaux gauche et droit
left_array_length = mid_index - left_index 1
longueur_du_tableau_droit = indice_droit - indice_milieu
## index pour la fusion de deux tableaux
i = j = 0
## index pour le remplacement des éléments du tableau
k = indice_gauche
## itération sur les deux sous-réseaux
while i < left_array_length et j < right_array_length :
## comparer les éléments des tableaux de gauche et de droite
if left_array<x><x><x><x><x>[i]</x></x></x></x></x> < right_array<x><x><x><x><x>[j]</x></x></x></x></x>:
arr<x><x>[k]</x></x> = left_array<x><x><x><x><x>[i]</x></x></x></x></x>
i = 1
sinon :
arr[<x><x>k]</x></x> = right_array<x><x><x><x><x>[j]</x></x></x></x></x>
j = 1
k = 1
## ajout des éléments restants des tableaux gauche et droit
while i < left_array_length :
arr<x><x>[k]</x></x> = left_array<x><x><x><x><x>[i]</x></x></x></x></x>
i = 1
k = 1
while j < right_array_length :
j = 1
k = 1
def merge_sort(arr, left_index, right_index) :
## cas de base pour une fonction récursive
si indice_gauche >= indice_droit :
retour
## recherche de l'indice moyen
mid_index = (left_index right_index) // 2
## appels récursifs
merge_sort(arr, indice_gauche, indice_milieu)
merge_sort(arr, mid_index 1, right_index)
## fusionner les deux sous-ensembles
merge(arr, left_index, mid_index, right_index)
if __name__ == '__main__' :
## Initialisation du tableau
arr = [3, 4, 7, 8, 1, 9, 5, 2, 6]
merge_sort(arr, 0, 8)
## impression du tableau
print(str(arr))Conclusion
Il existe de nombreux autres algorithmes de tri, mais les algorithmes ci-dessus sont parmi les plus fréquemment utilisés. J’espère que vous avez apprécié l’apprentissage du tri.
Découvrez ensuite les algorithmes de recherche.
Bon codage 🙂 👨💻

