In diesem Lernprogramm lernen Sie, wie Sie zwei Matrizen in Python multiplizieren können.
Zunächst lernen Sie die Bedingungen für eine gültige Matrixmultiplikation kennen und schreiben eine benutzerdefinierte Python-Funktion zur Multiplikation von Matrizen. Als Nächstes werden Sie sehen, wie Sie dasselbe Ergebnis mit verschachtelten Listenauflösungen erreichen können.
Schließlich werden Sie NumPy und seine eingebauten Funktionen verwenden, um die Matrixmultiplikation effizienter durchzuführen.
Wie Sie prüfen, ob die Matrixmultiplikation gültig ist
Bevor Sie Python-Code für die Matrixmultiplikation schreiben, lassen Sie uns noch einmal die Grundlagen der Matrixmultiplikation durchgehen.
Eine Matrixmultiplikation zwischen zwei Matrizen A und B ist nur dann gültig, wenn die Anzahl der Spalten in Matrix A gleich der Anzahl der Zeilen in Matrix B ist.
Diese Bedingung für die Matrixmultiplikation ist Ihnen wahrscheinlich schon einmal begegnet. Aber haben Sie sich jemals gefragt, warum dies der Fall ist?
Nun, es liegt an der Art und Weise, wie die Matrixmultiplikation funktioniert. Werfen Sie einen Blick auf das Bild unten.
In unserem allgemeinen Beispiel hat die Matrix A m Zeilen und n Spalten. Und Matrix B hat n Zeilen und p Spalten.

Was ist die Form der Produktmatrix?
Das Element am Index (i, j) in der resultierenden Matrix C ist das Punktprodukt der Zeile i der Matrix A und der Spalte j der Matrix B.
Um also ein Element bei einem bestimmten Index in der resultierenden Matrix C zu erhalten, müssen Sie das Punktprodukt der entsprechenden Zeile und Spalte in den Matrizen A bzw. B berechnen.
Wenn Sie den obigen Vorgang wiederholen, erhalten Sie die Produktmatrix C der Form m x p – mit m Zeilen und p Spalten, wie unten dargestellt.

Und das Punktprodukt oder das innere Produkt zwischen zwei Vektoren a und b wird durch die folgende Gleichung gegeben.

Lassen Sie uns zusammenfassen:
- Es ist offensichtlich, dass das Punktprodukt nur zwischen Vektoren mit gleicher Länge definiert ist.
- Damit das Punktprodukt zwischen einer Zeile und einer Spalte gültig ist – wenn Sie zwei Matrizen multiplizieren -, müssen beide die gleiche Anzahl von Elementen haben.
- In dem obigen allgemeinen Beispiel hat jede Zeile der Matrix A n Elemente. Und jede Spalte in Matrix B hat ebenfalls n Elemente.
Wenn Sie genauer hinsehen, ist n die Anzahl der Spalten in Matrix A und auch die Anzahl der Zeilen in Matrix B. Und das ist genau der Grund, warum die Anzahl der Spalten in Matrix A gleich der Anzahl der Zeilen in Matrix B sein muss.
Ich hoffe, Sie haben die Bedingung für die Gültigkeit der Matrixmultiplikation verstanden und wissen, wie Sie jedes Element der Produktmatrix erhalten.
Lassen Sie uns nun etwas Python-Code schreiben, um zwei Matrizen zu multiplizieren.
Schreiben Sie eine benutzerdefinierte Python-Funktion zur Multiplikation von Matrizen
Als ersten Schritt schreiben wir eine benutzerdefinierte Funktion zum Multiplizieren von Matrizen.
Diese Funktion sollte Folgendes tun:
- Sie akzeptiert zwei Matrizen, A und B, als Eingaben.
- Prüfen Sie, ob die Matrixmultiplikation zwischen A und B gültig ist.
- Wenn ja, multiplizieren Sie die beiden Matrizen A und B und geben Sie die Produktmatrix C zurück.
- Andernfalls geben Sie eine Fehlermeldung zurück, dass die Matrizen A und B nicht multipliziert werden können.
Schritt 1: Erzeugen Sie zwei Matrizen aus ganzen Zahlen mit der Funktion random.randint() von NumPy. Sie können Matrizen auch als verschachtelte Python-Listen deklarieren.
import numpy as np
np.random.seed(27)
A = np.random.randint(1,10,size = (3,3))
B = np.random.randint(1,10,size = (3,2))
print(f "Matrix A:\n {A}\n")
print(f "Matrix B:\n {B}\n")
# Ausgabe
Matrix A:
[[4 9 9]
[9 1 6]
[9 2 3]]
Matrix B:
[[2 2]
[5 7]
[4 4]]Schritt 2: Fahren Sie fort und definieren Sie die Funktion multiply_matrix(A,B). Diese Funktion nimmt zwei Matrizen A und B als Eingaben entgegen und gibt die Produktmatrix C zurück, wenn die Matrixmultiplikation gültig ist.
def multiply_matrix(A,B):
global C
if A.form<x><x><x>[1]</x></x></x> == B.form<x><x><x>[0]</x></x></x>:
C = np.zeros((A.form<x><x><x>[0]</x></x></x>,B.form<x><x><x>[1]</x></x></x>),dtype = int)
for row in range(rows):
for col in range(cols):
for elt in range(len(B)):
C[Zeile, Spalte] = A[Zeile, elt] * B[elt, Spalte]
return C
sonst:
return "Sorry, kann A und B nicht multiplizieren."Parsen der Funktionsdefinition
Fahren wir fort mit dem Parsen der Funktionsdefinition.
Deklarieren Sie C als eine globale Variable: Standardmäßig haben alle Variablen innerhalb einer Python-Funktion einen lokalen Geltungsbereich. Und Sie können von außerhalb der Funktion nicht auf sie zugreifen. Um die Produktmatrix C von außen zugänglich zu machen, müssen wir sie als globale Variable deklarieren. Fügen Sie einfach den globalen Qualifizierer vor den Variablennamen.
Prüfen Sie, ob die Matrixmultiplikation gültig ist: Verwenden Sie das Attribut shape, um zu prüfen, ob A und B multipliziert werden können. Für jedes Array arr geben arr.shape<x><x><x>[0]</x></x></x> und arr.shape<x><x><x>[1]</x></x></x> die Anzahl der Zeilen bzw. Spalten an. Wenn also A.shape<x><x><x>[1]</x></x></x> == B.shape<x><x><x>[0]</x></x></x> ist, wird geprüft, ob die Matrixmultiplikation gültig ist. Nur wenn diese Bedingung True ist, wird die Produktmatrix berechnet. Andernfalls gibt die Funktion eine Fehlermeldung zurück.
Verwenden Sie verschachtelte Schleifen, um Werte zu berechnen: Um die Elemente der resultierenden Matrix zu berechnen, müssen wir die Zeilen der Matrix A in einer Schleife durchlaufen, und die äußere for-Schleife übernimmt diese Aufgabe. Die innere for-Schleife hilft uns, die Spalten der Matrix B zu durchlaufen. Und die innerste for-Schleife hilft uns, auf jedes Element in der ausgewählten Spalte zuzugreifen.
▶️ Nachdem wir nun gelernt haben, wie die Python-Funktion zum Multiplizieren von Matrizen funktioniert, rufen wir die Funktion mit den Matrizen A und B auf, die wir zuvor erzeugt haben.
multiply_matrix(A,B)
# Ausgabe
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])Da die Matrixmultiplikation zwischen A und B gültig ist, gibt die Funktion multiply_matrix() die Produktmatrix C zurück.
Python Nested List Comprehension zur Multiplikation von Matrizen verwenden
Im vorherigen Abschnitt haben Sie eine Python-Funktion zur Multiplikation von Matrizen geschrieben. Jetzt werden Sie sehen, wie Sie verschachtelte Listenverknüpfungen verwenden können, um das Gleiche zu tun.
Hier ist die verschachtelte Listenverarbeitung zum Multiplizieren von Matrizen.
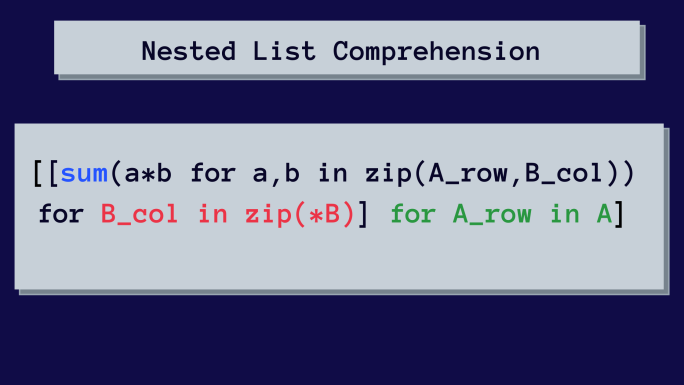
Auf den ersten Blick mag das kompliziert aussehen. Aber wir werden das verschachtelte Listenverständnis Schritt für Schritt analysieren.
Konzentrieren wir uns jeweils auf ein Listenverständnis und ermitteln, was es tut.
Wir verwenden die folgende allgemeine Vorlage für das Listenverständnis:
[<Dieses> für <Element> in <Aufzählbar>]
wobei,
<do-this>: was Sie tun möchten - Ausdruck oder Operation
<Element>: jedes Element, für das Sie die Operation durchführen möchten
<iterable>: die Iterable (Liste, Tupel, etc.), durch die Sie eine Schleife ziehen▶️ Lesen Sie unseren Leitfaden Listenverständnis in Python – mit Beispielen, um ein tieferes Verständnis zu erlangen.
Bevor Sie fortfahren, beachten Sie bitte, dass wir die resultierende Matrix C Zeile für Zeile aufbauen möchten.
Verschachtelte Listenverknüpfung erklärt
Schritt 1: Berechnen Sie einen einzelnen Wert in der Matrix C
Ausgehend von der Zeile i der Matrix A und der Spalte j der Matrix B gibt der folgende Ausdruck den Eintrag bei Index (i, j) in der Matrix C an.
sum(a*b for a,b in zip(A_row, B_col)
# zip(A_row, B_col) gibt einen Iterator von Tupeln zurück
# Wenn A_row = [a1, a2, a3] & B_col = [b1, b2, b3]
# gibt zip(A_row, B_col) (a1, b1), (a2, b2), und so weiterWenn i= j = 1 ist, gibt der Ausdruck den Eintrag c_11 der Matrix C zurück. Auf diese Weise können Sie also ein Element in einer Zeile erhalten.
Schritt 2: Bilden Sie eine Zeile in der Matrix C
Unser nächstes Ziel ist es, eine ganze Zeile zu bilden.
Für Zeile 1 in Matrix A müssen Sie eine Schleife durch alle Spalten in Matrix B ziehen, um eine komplette Zeile in Matrix C zu erhalten.
Gehen Sie zurück zur Vorlage für das Listenverständnis.
- Ersetzen Sie
<do-this>durch den Ausdruck aus Schritt 1, denn das ist es, was Sie tun wollen. - Als nächstes ersetzen Sie
<item>durchB_col - jedeSpalte in Matrix B. - Ersetzen Sie schließlich
<iterable>durchzip(*B)-die Liste mit allen Spalten der Matrix B.
Und hier ist das erste Listenverständnis.
[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
# zip(*B): * ist der Entpackungsoperator
# zip(*B) gibt eine Liste der Spalten der Matrix B zurückSchritt 3: Bauen Sie alle Zeilen auf und erhalten Sie die Matrix C
Als nächstes müssen Sie die Produktmatrix C auffüllen, indem Sie die restlichen Zeilen berechnen.
Dazu müssen Sie eine Schleife durch alle Zeilen der Matrix A ziehen.
Gehen Sie noch einmal zum Listenverständnis zurück und tun Sie Folgendes.
- Ersetzen Sie
<do-this>durch das Listenverständnis aus Schritt 2. Erinnern Sie sich, dass wir im vorherigen Schritt eine ganze Zeile berechnet haben. - Ersetzen Sie nun
<item>durchA_row - jedeZeile der Matrix A. - Und Ihr
<iterable>ist die Matrix A selbst, da Sie in einer Schleife durch ihre Zeilen gehen.
Und hier ist unser endgültiges verschachteltes Listen-Verständnis.🎊
[[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A]Es ist an der Zeit, das Ergebnis zu überprüfen! ✔
# in NumPy-Array umwandeln mit np.array()
C = np.array([[sum(a*b for a,b in zip(A_row, B_col)) for B_col in zip(*B)]
for A_row in A])
# Ausgabe:
[[ 89 107]
[ 47 49]
[ 40 44]]Wenn Sie genauer hinsehen, entspricht dies den verschachtelten for-Schleifen, die wir zuvor hatten – nur dass es noch prägnanter ist.
Außerdem können Sie dies mit Hilfe einiger eingebauter Funktionen noch effizienter machen. Diese lernen wir im nächsten Abschnitt kennen.
Verwenden Sie NumPy matmul() zum Multiplizieren von Matrizen in Python
Die Funktion np.matmul() nimmt zwei Matrizen als Eingabe entgegen und gibt das Produkt zurück, wenn die Matrixmultiplikation zwischen den eingegebenen Matrizen gültig ist.
C = np.matmul(A,B)
print(C)
# Ausgabe:
[[ 89 107]
[ 47 49]
[ 40 44]]Beachten Sie, dass diese Methode einfacher ist als die beiden Methoden, die wir zuvor gelernt haben. Tatsächlich können Sie anstelle von np.matmul() einen äquivalenten @-Operator verwenden, und das werden wir gleich sehen.
Wie man den @-Operator in Python zum Multiplizieren von Matrizen verwendet
In Python ist @ ein binärer Operator, der für die Multiplikation von Matrizen verwendet wird.
Er arbeitet mit zwei Matrizen und im Allgemeinen mit N-dimensionalen NumPy-Arrays und gibt die Produktmatrix zurück.
Hinweis: Sie benötigen Python 3.5 oder höher, um den
@-Operatorzu verwenden.
Hier sehen Sie, wie Sie ihn verwenden können.
C = A@B
print(C)
# Ausgabe
array([[ 89, 107],
[ 47, 49],
[ 40, 44]])Beachten Sie, dass die Produktmatrix C die gleiche ist wie die, die wir zuvor erhalten haben.
Können Sie np.dot() zum Multiplizieren von Matrizen verwenden?
Wenn Sie schon einmal auf einen Code gestoßen sind, der np.dot() zum Multiplizieren zweier Matrizen verwendet, dann wissen Sie jetzt, wie es funktioniert.
C = np.dot(A,B)
print(C)
# Ausgabe:
[[ 89 107]
[ 47 49]
[ 40 44]]Sie werden sehen, dass np.dot(A, B) auch die erwartete Produktmatrix zurückgibt.
Wie in den NumPy-Dokumenten beschrieben, sollten Sie np.dot() jedoch nur zur Berechnung des Punktprodukts zweier eindimensionaler Vektoren verwenden und nicht zur Matrixmultiplikation.
Erinnern Sie sich an den vorherigen Abschnitt: Das Element mit dem Index (i, j) der Produktmatrix C ist das Punktprodukt der Zeile i der Matrix A und der Spalte j der Matrix B.
Da NumPy diese Punktprodukt-Operation implizit auf alle Zeilen und alle Spalten überträgt, erhalten Sie die resultierende Produktmatrix. Um Ihren Code jedoch lesbar zu halten und Mehrdeutigkeiten zu vermeiden, verwenden Sie stattdessen np.matmul() oder den @-Operator.
Fazit
🎯 In diesem Tutorial haben Sie das Folgende gelernt.
- Bedingung für eine gültige Matrixmultiplikation: Anzahl der Spalten in Matrix A = Anzahl der Zeilen in Matrix B.
- Wie Sie eine benutzerdefinierte Python-Funktion schreiben, die prüft, ob die Matrixmultiplikation gültig ist und die Produktmatrix zurückgibt. Der Hauptteil der Funktion verwendet verschachtelte for-Schleifen.
- Als Nächstes haben Sie gelernt, wie Sie verschachtelte Listenverknüpfungen verwenden, um Matrizen zu multiplizieren. Sie sind prägnanter als for-Schleifen, aber anfällig für Probleme mit der Lesbarkeit.
- Schließlich haben Sie gelernt, wie Sie die in NumPy integrierte Funktion np.matmul() zum Multiplizieren von Matrizen verwenden können und dass dies in Bezug auf die Geschwindigkeit am effizientesten ist.
- Sie haben auch den @-Operator zum Multiplizieren zweier Matrizen in Python kennen gelernt.
Damit ist unsere Diskussion über die Matrixmultiplikation in Python abgeschlossen. Als nächsten Schritt lernen Sie, wie Sie in Python prüfen können, ob eine Zahl eine Primzahl ist. Oder lösen Sie interessante Probleme mit Python-Strings.
Viel Spaß beim Lernen!🎉

