Cómo comprobar si un número es primo en Python

Este tutorial le enseñará a escribir un programa en Python para comprobar si un número es primo o no.

Si alguna vez ha realizado pruebas de codificación, se habrá encontrado con la pregunta matemática sobre la prueba de primalidad o para comprobar si un número es primo. Y en los próximos minutos, aprenderá a dar con la solución óptima a esta pregunta.

En este tutorial, usted

repasará los conceptos básicos de los números primos,
escribirá código Python para comprobar si un número es primo, y
optimizarlo aún más para obtener un algoritmo de tiempo de ejecución O(√n).

Por todo esto y más, empecemos.

¿Qué es un número primo?

Empecemos repasando los conceptos básicos de los números primos.

En teoría numérica, se dice que un número natural n es primo si tiene exactamente dos factores: 1 y el propio número(n). Recordemos de las matemáticas de su colegio: se dice que un número i es un factor del número n, si i divide a n en partes iguales. ✅

La siguiente tabla enumera algunos números, todos sus factores y si son primos.

n	Factores	¿Es primo?
1	1	No
2	1, 2	Sí
3	1, 3	Sí
4	1, 2, 4	No
7	1, 7	Sí
15	1, 3, 5, 15	No

A partir de la tabla anterior, podemos anotar lo siguiente:

2 es el número primo más pequeño.
1 es un factor de cada número.
Todo número n es factor de sí mismo.

Así que 1 y n son factores triviales para cualquier número n. Y un número primo no debe tener más factores que estos dos.

Esto significa que al pasar de 2 a n – 1, no debería poder encontrar un factor no trivial que divida a n sin resto.

Algoritmo O(n) para comprobar si un número es primo en Python

En esta sección, vamos a formalizar el planteamiento anterior en una función de Python.

Puede hacer un bucle a través de todos los números de 2 a n – 1 utilizando el objeto range () en Python.

En Python, range(inicio, parada, paso) devuelve un objeto range. A continuación, puede iterar sobre el objeto range para obtener una secuencia desde inicio hasta parada -1 en pasos de paso.

Dado que necesitamos el conjunto de enteros de 2 a n-1, podemos especificar range (2, n) y utilizarlo junto con el bucle for.

Esto es lo que nos gustaría hacer

Si encuentra un número que divida n uniformemente sin resto, puede concluir inmediatamente que el número no es primo.

Si ha recorrido todo el rango de números desde 2 hasta n – 1 sin encontrar un número que divida n uniformemente, entonces el número es primo.

Función de Python para comprobar si un número es primo

Usando lo anterior, podemos seguir adelante y definir la función is_prime () como sigue.

def es_primo(n):
  for i in range(2,n):
    if (n%i) == 0:
      return False
  return True

Analicemos ahora la definición de la función anterior.

La función anterior es_primo( ) toma un entero positivo n como argumento.
Si encuentra un factor en el intervalo especificado de (2, n-1), la función devuelve Falso , ya queel número no es primo.
Y devuelve Verdadero si recorre todo el bucle sin encontrar un factor.

A continuación, llamemos a la función con argumentos y verifiquemos si la salida es correcta.

es_primo(2)
# Verdadero

es_primo(8)
# Falso

es_primo(9)
# Falso

es_primo(11)
# Verdadero

En la salida anterior, se ve que 2 y 11 son primos (la función devuelve True). Y 8 y 9 no son primos (la función devuelve Falso).

Cómo optimizar la función de Python is_prime()

Aquí podemos hacer una pequeña optimización. Observe la lista de factores en la siguiente tabla.

Número	Factores
6	1, 2, 3, 6
10	1, 2, 5, 10
18	1, 2, 3, 6 , 9, 18

Bien, podemos ver que el único factor de n que es mayor que n/2 es el propio n.

Así que esto significa que no tiene que hacer el bucle hasta n – 1. En su lugar, puede ejecutar el bucle sólo hasta n/2.

Si no encuentra un factor no trivial hasta n/2, tampoco podrá encontrarlo más allá de n/2.

Ahora modifiquemos la función es_primo () para buscar factores en el intervalo (2, n/2)

def es_primo(n):
  for i in range(2,int(n/2)):
    if (n%i) == 0:
      return False
  return True

Sigamos adelante y verifiquemos la salida mediante unas cuantas llamadas a funciones.

es_primo(9)
# falso

es_primo(11)
# True

Aunque pueda parecer que hemos optimizado, este algoritmo no es más eficiente que el anterior en términos de complejidad de tiempo de ejecución. De hecho, ambos tienen una complejidad de tiempo de ejecución O(n): proporcional al valor de n o lineal en n.

¿Podemos hacerlo mejor? Sí, ¡podemos!

▶️ Pase a la siguiente sección para determinar cómo mejorar la complejidad temporal de la comprobación de números primos.

Algoritmo O(√n) para comprobar un número primo en Python

Sucede que los factores de un número se dan por pares.

Si a es un factor del número n, entonces también existe un factor b tal que a x b = n, o simplemente, ab = n.

Verifiquemos esto mediante un ejemplo.

La tabla siguiente muestra los factores del número 18 que aparecen por pares. Si lo desea, puede verificar lo mismo para algunos números más.

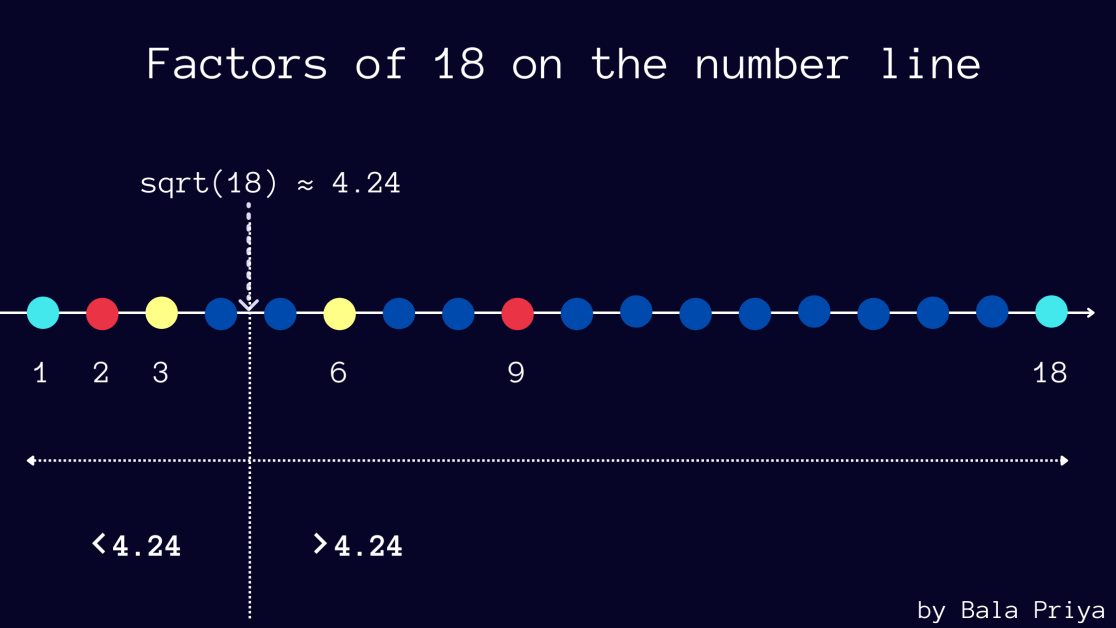
Observe también que √18 es aproximadamente 4,24.

Y en los factores que ocurren en pares (a, b), puede ver que si a es menor que 4,24, entonces b es mayor que 4,24-en este ejemplo, (2, 18) y (3, 6).

a	b
1	18
2	9
3	6

Factores de 18 en pares

La siguiente figura muestra los factores de 18 trazados en la recta numérica.

Si el número n resulta ser un cuadrado perfecto, tendrá a = b = √n como uno de los factores.

▶️ Observe los factores de 36 en la tabla siguiente. Como 36 es un cuadrado perfecto, a = b = 6 es uno de los factores. Para todos los demás pares de factores (a, b), se cumple que a 6.

a	b
1	36
2	18
3	12
4	9
6	6

Factores de 36 en pares

Resumiendo, tenemos lo siguiente

Todo número n puede escribirse como n = a x b
Si n es un cuadrado perfecto, entonces a = b = √n.
Y si a < b, entonces, a < √n y b > √n.
Si no, si a > b, entonces a > √n y b< √n.

Así que en lugar de recorrer todos los enteros hasta n/2, puede optar por recorrer hasta √n. Y esto es mucho más eficiente que nuestro enfoque anterior.

Cómo modificar is_prime() a algoritmo O(√n)

Procedamos a optimizar la función para buscar números primos en Python.


import math
def es_primo(n):
  for i in range(2,int(math.sqrt(n)) 1):
    if (n%i) == 0:
      return False
  devolver True

Ahora, analicemos la definición de la función anterior:

Para calcular la raíz cuadrada de un número, importemos el módulo matemático incorporado de Python y utilicemos la función math .sqrt().
Como n puede no ser un cuadrado perfecto, tendremos que convertirlo en un número entero. Utilice int(var) para convertir var en un entero.
Para asegurarnos de que realmente estamos comprobando hasta √n, añadimos un más uno, ya que la función range () excluye por defecto el punto final del rango.

La celda de código siguiente verifica que nuestra función is_prime ( ) funciona correctamente.

is_prime(8)
# Falso

is_prime(15)
# Falso

es_primo(23)
# Verdadero

En la siguiente sección, vamos a crear unos cuantos gráficos sencillos para entender O(n) y O(√n) visualmente.

Comparación visual de O(n) y O(√n)

▶️ Ejecute el siguiente fragmento de código en un entorno de cuaderno Jupyter de su elección.

import numpy as np
import seaborn as sns
import pandas as pd


n = 20

x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1, "O(n)":y2})
sns.set_theme()
sns.lineplot(datos = df)

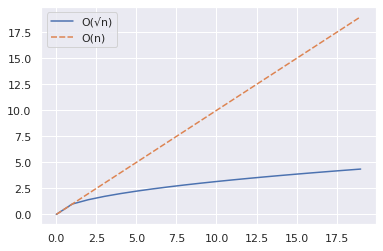
El fragmento anterior muestra cómo se pueden trazar las curvas de n y √n para un rango de valores.

Utilizamos la función NumPy arange() para crear una matriz de números.
Y luego, recogemos los valores de n y √n hasta, pero sin incluir 20, en un pandas DataFrame.
A continuación, trazamos utilizando la función lineplot() de seaborn.

En el gráfico siguiente, vemos que √n es significativamente menor que n.

Aumentemos ahora el rango hasta 2000 y repitamos los mismos pasos anteriores.

import numpy como np
import seaborn as sns
import pandas as pd


n = 2000

x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1, "O(n)":y2})
sns.set_theme()
sns.lineplot(datos = df)

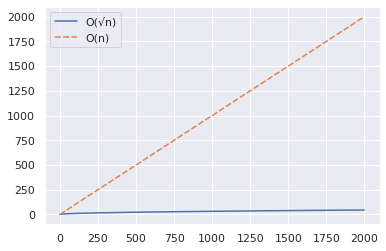
Del gráfico anterior, puede deducir que el algoritmo O(√n) es significativamente más rápido cuando se trata de comprobar si un número grande es primo.

He aquí un ejemplo rápido: ¡2377 es un número primo-verifíquelo!😀

Mientras que el enfoque O(n) le llevará del orden de 2000 pasos, el algoritmo O(√n) puede ayudarle a llegar a la respuesta en sólo 49 pasos.✅

Conclusión

⏳ Y es hora de un resumen rápido.

Para comprobar si un número es primo, el enfoque ingenuo consiste en recorrer en bucle todos los números del intervalo (2, n-1). Si no encuentra un factor que divida a n, entonces n es primo.
Como el único factor de n mayor que n/2 es el propio n, puede optar por recorrer sólo hasta n/2.
Ambos enfoques tienen una complejidad temporal de O(n).
Como los factores de un número se dan por pares, puede ejecutar sólo hasta √n. Este algoritmo es mucho más rápido que O(n). Y la ganancia es apreciable al comprobar si un número grande es primo o no.

Espero que haya entendido cómo comprobar si un número es primo en Python. Como siguiente paso, puede consultar nuestro tutorial sobre programas de Python sobre operaciones con cadenas, dondeaprenderá a comprobar si las cadenas son palíndromos, anagramas y mucho más.

Nos vemos en otro tutorial. Hasta entonces, ¡feliz codificación!👩🏽‍💻

Bala Priya C
Colaborador
Bala Priya es una desarrolladora y redactora técnica india con más de tres años de experiencia en la redacción de contenidos técnicos. Comparte sus conocimientos con la comunidad de desarrolladores escribiendo tutoriales técnicos, guías prácticas y mucho más. Actualmente trabaja como editora técnica en Geekflare. También colabora activamente en otras publicaciones técnicas como freeCodeCamp y KDnuggets.