Qu’est-ce qu’une matrice de confusion dans l’apprentissage automatique ?

Une matrice de confusion est un outil permettant d’évaluer les performances du type de classification des algorithmes d’apprentissage automatique supervisé.

Qu’est-ce qu’une matrice de confusion ?

Nous, les humains, percevons les choses différemment – même la vérité et les mensonges. Ce qui peut me sembler être une ligne de 10 cm de long peut vous sembler être une ligne de 9 cm. Mais la valeur réelle peut être 9, 10 ou autre chose. Ce que nous devinons est la valeur prédite !

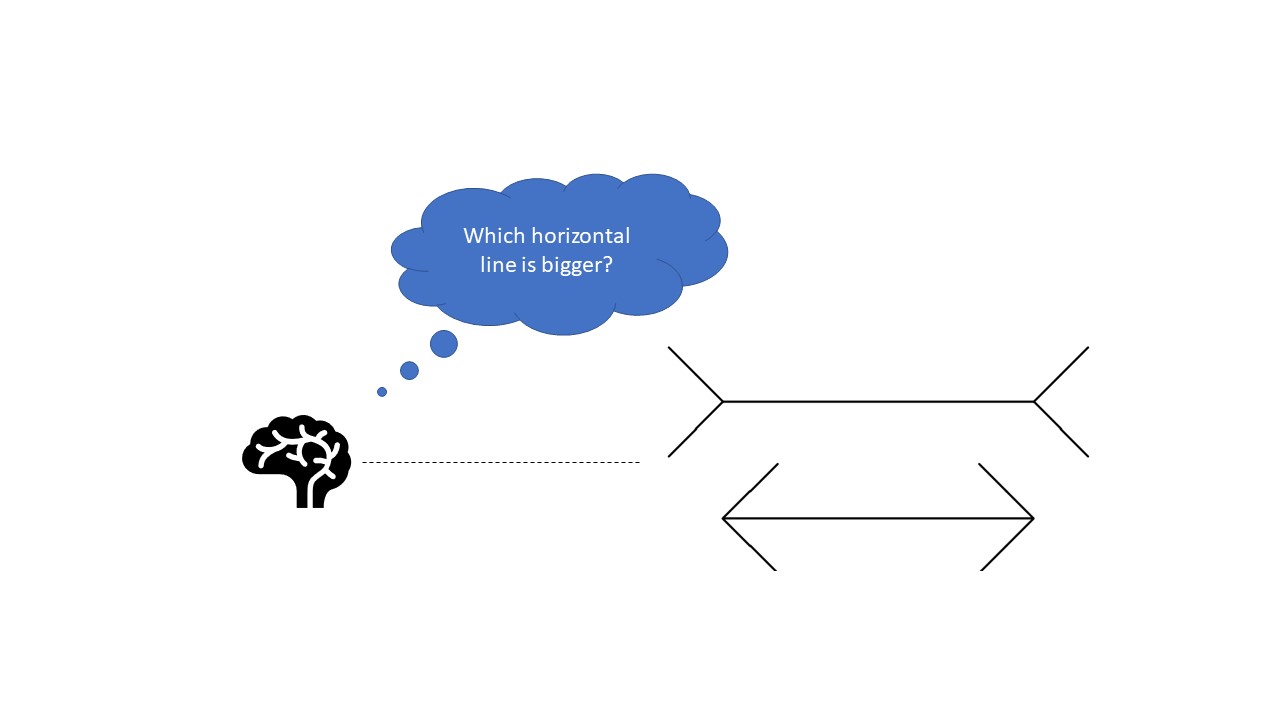
Tout comme notre cerveau applique sa propre logique pour prédire quelque chose, les machines appliquent divers algorithmes (appelés algorithmes d’apprentissage automatique ) pour parvenir à une valeur prédite pour une question. Là encore, ces valeurs peuvent être identiques ou différentes de la valeur réelle.

Dans un monde compétitif, nous aimerions savoir si notre prédiction est correcte ou non pour comprendre notre performance. De la même manière, nous pouvons déterminer la performance d’un algorithme d’apprentissage automatique en fonction du nombre de prédictions qu’il a faites correctement.

Qu’est-ce qu’un algorithme d’apprentissage automatique ?

Les machines tentent d’obtenir certaines réponses à un problème en appliquant une certaine logique ou un ensemble d’instructions, appelées algorithmes d’apprentissage automatique. Les algorithmes d’apprentissage automatique sont de trois types : supervisés, non supervisés ou de renforcement.

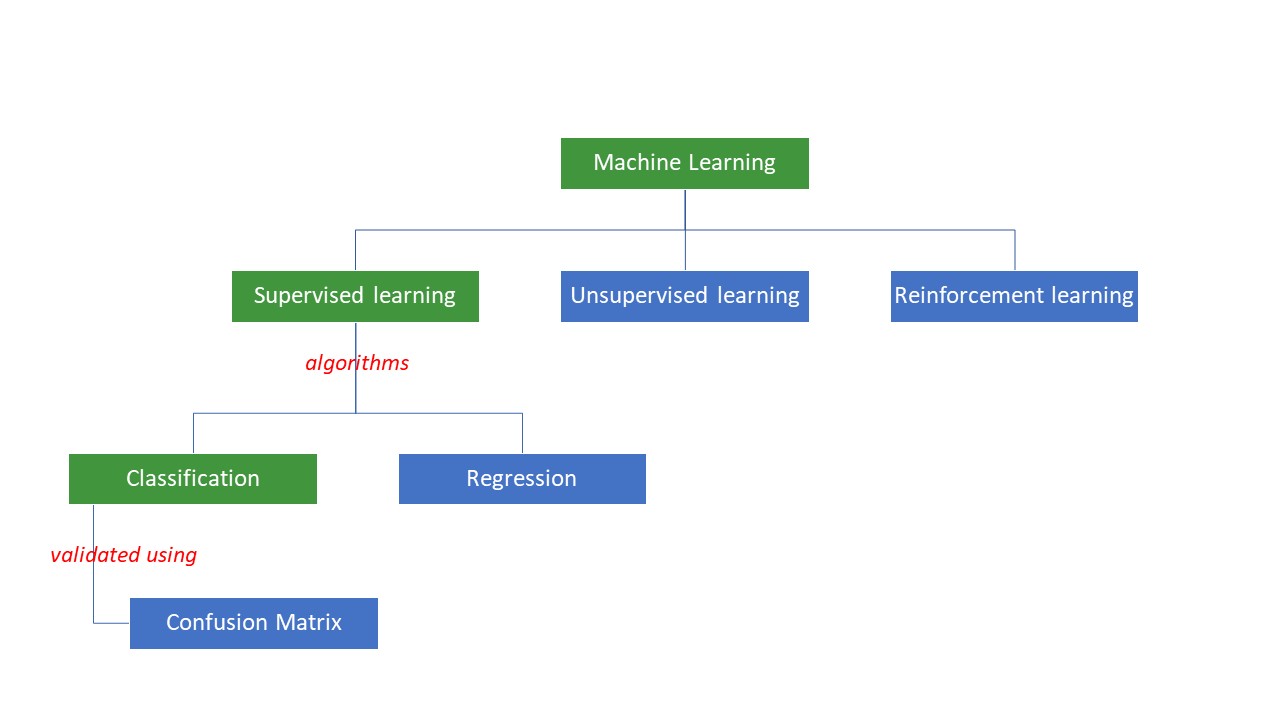
Les types d’algorithmes les plus simples sont les algorithmes supervisés, dans lesquels nous connaissons déjà la réponse et nous entraînons les machines à parvenir à cette réponse en entraînant l’algorithme avec un grand nombre de données – de la même manière qu’un enfant différencierait des personnes de groupes d’âge différents en examinant leurs caractéristiques à plusieurs reprises.

Les algorithmes ML supervisés sont de deux types : la classification et la régression.

Les algorithmes de classification classent ou trient les données en fonction d’un ensemble de critères. Par exemple, si vous souhaitez que votre algorithme regroupe les clients en fonction de leurs préférences alimentaires – ceux qui aiment la pizza et ceux qui ne l’aiment pas -, vous utiliserez un algorithme de classification tel que l’arbre de décision, la forêt aléatoire, les Bayes naïfs ou le SVM(Support Vector Machine).

Lequel de ces algorithmes serait le plus performant ? Pourquoi devriez-vous choisir un algorithme plutôt qu’un autre ?

Entrez dans la matrice de confusion….

Une matrice de confusion est une matrice ou un tableau qui donne des informations sur la précision d’un algorithme de classification dans la classification d’un ensemble de données. Le nom n’a pas pour but d’embrouiller les humains, mais un trop grand nombre de prédictions incorrectes signifie probablement que l’algorithme était confus😉 !

Une matrice de confusion est donc une méthode d’évaluation de la performance d’un algorithme de classification.

Comment ?

Supposons que vous appliquiez différents algorithmes à notre problème binaire mentionné précédemment : classer (séparer) les personnes selon qu’elles aiment ou n’aiment pas les pizzas. Pour évaluer l’algorithme dont les valeurs sont les plus proches de la bonne réponse, vous utiliserez une matrice de confusion. Pour un problème de classification binaire (aimer/désaimer, vrai/faux, 1/0), la matrice de confusion donne quatre valeurs de grille, à savoir :

• Vrai positif (VP)
• Vrai négatif (VN)
• Faux positif (FP)
• Faux négatif (FN)

Quelles sont les quatre grilles d’une matrice de confusion ?

Les quatre valeurs déterminées à l’aide de la matrice de confusion forment les grilles de la matrice.

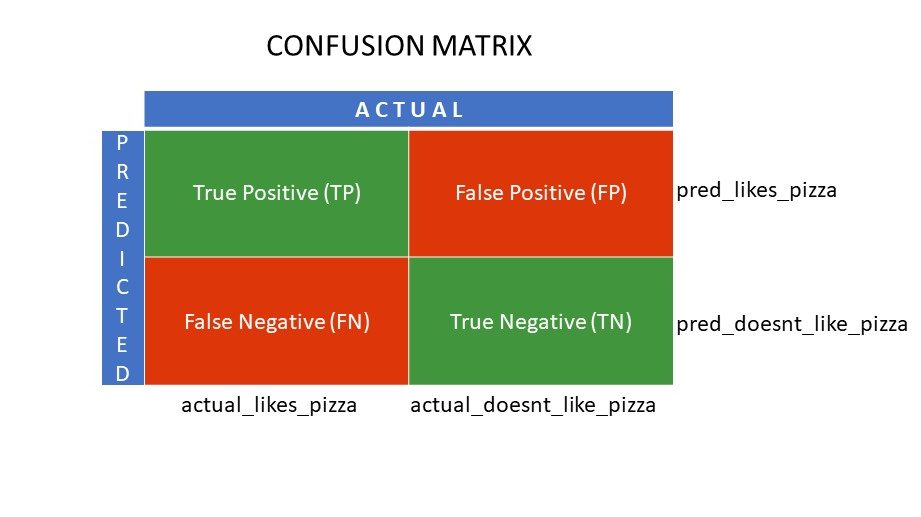
Les vrais positifs (TP) et les vrais négatifs (TN) sont les valeurs correctement prédites par l’algorithme de classification,

• TP représente les personnes qui aiment la pizza et que le modèle a correctement classées,
• TN représente les personnes qui n’aiment pas la pizza et que le modèle a classées correctement,

Les faux positifs (FP) et les faux négatifs (FN) sont les valeurs prédites à tort par le classificateur,

• FP représente les personnes qui n’aiment pas la pizza (négatif), mais le classificateur a prédit qu’elles aimaient la pizza (positif à tort). FP est également appelée erreur de type I.
• FN représente ceux qui aiment la pizza (positif), mais le classificateur a prédit qu’ils ne l’aimaient pas (négatif à tort). FN est également appelée erreur de type II.

Pour mieux comprendre ce concept, prenons un exemple concret.

Supposons que vous disposiez d’un ensemble de données de 400 personnes ayant subi le test Covid. Vous avez ensuite obtenu les résultats de différents algorithmes qui ont déterminé le nombre de personnes Covid positives et Covid négatives.

Voici les deux matrices de confusion pour comparaison :

En regardant les deux, vous pourriez être tenté de dire que le^1er algorithme est plus précis. Mais pour obtenir un résultat concret, nous avons besoin d’indicateurs permettant de mesurer l’exactitude, la précision et bien d’autres valeurs qui prouvent que l’algorithme est meilleur.

Paramètres utilisant la matrice de confusion et leur importance

Les principales mesures qui nous aident à déterminer si le classificateur a fait les bonnes prédictions sont les suivantes :

#1. Rappel/Sensibilité

Le rappel, la sensibilité, le taux de vrais positifs (TPR) ou la probabilité de détection est le rapport entre les prédictions positives correctes (TP) et le nombre total de positifs (c’est-à-dire TP et FN).

R = TP/(TP FN)

Le rappel est la mesure des résultats positifs corrects renvoyés par rapport au nombre de résultats positifs corrects qui auraient pu être produits. Une valeur élevée de rappel signifie qu’il y a moins de faux négatifs, ce qui est bon pour l’algorithme. Utilisez le rappel lorsqu’il est important de connaître le nombre de faux négatifs. Par exemple, si une personne souffre de multiples blocages cardiaques et que le modèle montre qu’elle va très bien, cela peut s’avérer fatal.

#2. Précision

La précision est la mesure des résultats positifs corrects sur l’ensemble des résultats positifs prédits, y compris les vrais et les faux positifs.

Pr = TP/(TP FP)

La précision est très importante lorsque les faux positifs sont trop importants pour être ignorés. Par exemple, si une personne n’est pas diabétique, mais que le modèle le montre, et que le médecin lui prescrit certains médicaments. Cela peut entraîner des effets secondaires graves.

#3. La spécificité

La spécificité ou le taux de vrais négatifs (TNR) est le nombre de résultats négatifs corrects trouvés sur l’ensemble des résultats qui auraient pu être négatifs.

S = TN/(TN FP)

Il s’agit d’une mesure de l’efficacité avec laquelle votre classificateur identifie les valeurs négatives.

#4. Précision

La précision est le nombre de prédictions correctes par rapport au nombre total de prédictions. Ainsi, si vous avez trouvé correctement 20 valeurs positives et 10 valeurs négatives sur un échantillon de 50, la précision de votre modèle sera de 30/50.

Précision A = (TP TN)/(TP TN FP FN)

#5. Prévalence

La prévalence est la mesure du nombre de résultats positifs obtenus sur l’ensemble des résultats.

P = (TP FN)/(TP TN FP FN)

#6. Score F

Il est parfois difficile de comparer deux classificateurs (modèles) en utilisant uniquement la précision et le rappel, qui ne sont que des moyennes arithmétiques d’une combinaison des quatre grilles. Dans ce cas, nous pouvons utiliser le score F ou le score F1, qui est la moyenne harmonique – plus précise car elle ne varie pas trop pour des valeurs extrêmement élevées. Un score F élevé (max. 1) indique un meilleur modèle.

Score F = 2*Précision*Recall/ (Précision du rappel)

Lorsqu’il est vital de prendre en compte à la fois les faux positifs et les faux négatifs, le score F1 est une bonne mesure. Par exemple, il n’est pas nécessaire d’isoler inutilement les personnes qui ne sont pas covid positives (alors que l’algorithme l’a montré). De la même manière, ceux qui sont Covid positifs (mais l’algorithme a dit qu’ils ne l’étaient pas) doivent être isolés.

#7. Courbes ROC

Des paramètres tels que l’exactitude et la précision sont de bonnes mesures si les données sont équilibrées. Dans le cas d’un ensemble de données déséquilibré, une précision élevée ne signifie pas nécessairement que le classificateur est efficace. Par exemple, 90 étudiants sur 100 dans un lot connaissent l’espagnol. Même si votre algorithme indique que les 100 étudiants connaissent l’espagnol, sa précision sera de 90 %, ce qui peut donner une image erronée du modèle. Dans le cas d’ensembles de données déséquilibrés, des mesures telles que la courbe ROC sont des déterminants plus efficaces.

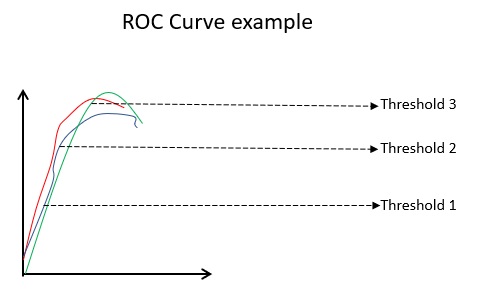
La courbe ROC(Receiver Operating Characteristic) affiche visuellement les performances d’un modèle de classification binaire à différents seuils de classification. Il s’agit d’un tracé du TPR (taux de vrais positifs) par rapport au FPR (taux de faux positifs), qui est calculé comme (1-Spécificité) à différentes valeurs de seuil. La valeur la plus proche de 45 degrés (en haut à gauche) dans le graphique est la valeur seuil la plus précise. Si le seuil est trop élevé, nous n’aurons pas beaucoup de faux positifs, mais nous aurons plus de faux négatifs et vice versa.

En général, lorsque la courbe ROC est tracée pour différents modèles, celui qui a la plus grande aire sous la courbe (AUC) est considéré comme le meilleur modèle.

Calculons toutes les valeurs métriques pour nos matrices de confusion du classificateur I et du classificateur II :

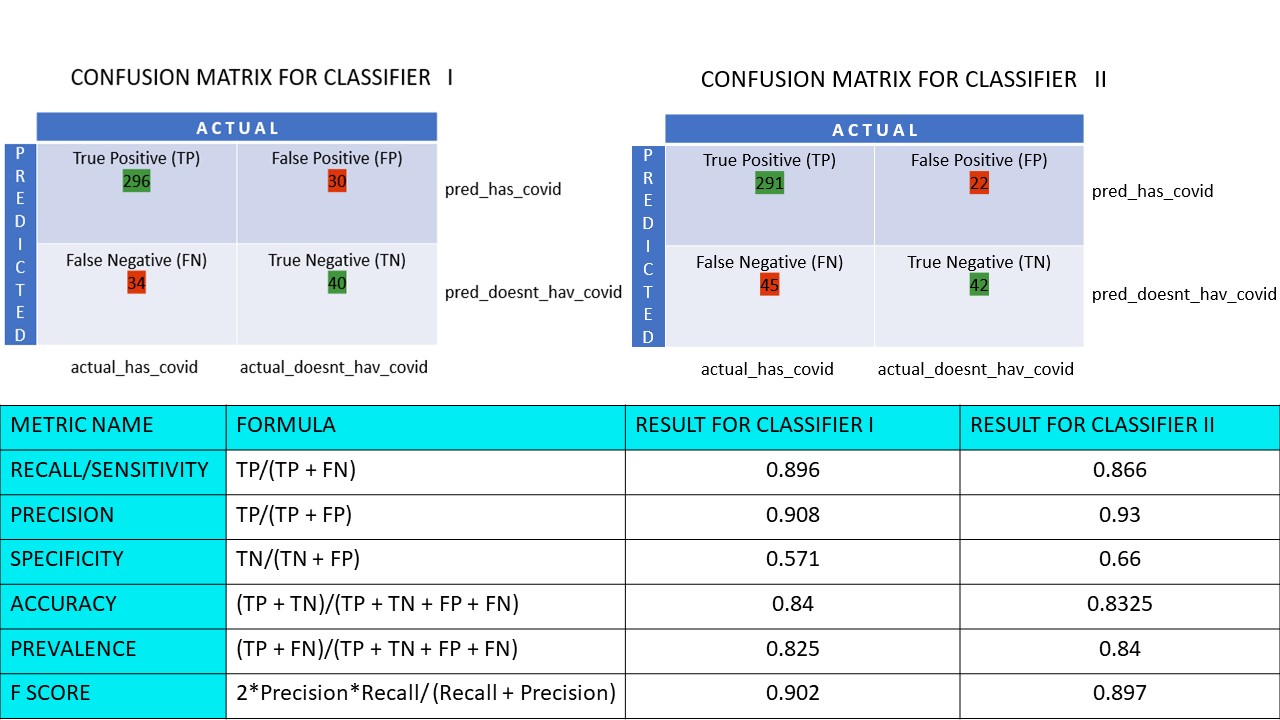
Nous constatons que la précision est plus élevée dans le classificateur II, tandis que l’exactitude est légèrement supérieure dans le classificateur I. En fonction du problème posé, les décideurs peuvent choisir les classificateurs I ou II.

Matrice de confusion N x N

Jusqu’à présent, nous avons vu une matrice de confusion pour les classificateurs binaires. Que se passerait-il s’il y avait plus de catégories que le simple oui/non ou le like/dislike ? Par exemple, si votre algorithme devait trier des images de couleurs rouge, verte et bleue. Ce type de classification est appelé classification multi-classes. Le nombre de variables de sortie détermine également la taille de la matrice. Ainsi, dans ce cas, la matrice de confusion sera de 3×3.

Résumé

Une matrice de confusion est un excellent système d’évaluation car elle fournit des informations détaillées sur les performances d’un algorithme de classification. Elle fonctionne bien pour les classificateurs binaires et multi-classes, lorsqu’il y a plus de deux paramètres à prendre en compte. Il est facile de visualiser une matrice de confusion, et nous pouvons générer toutes les autres mesures de performance comme le score F, la précision, le ROC et l’exactitude en utilisant la matrice de confusion.

Vous pouvez également consulter la rubrique Comment choisir des algorithmes de ML pour les problèmes de régression.