Comment vérifier si un nombre est premier en Python

Ce tutoriel vous apprendra à écrire un programme Python pour vérifier si un nombre est premier ou non.

Si vous avez déjà passé des tests de codage, vous avez certainement rencontré la question mathématique sur le test de primalité ou de vérifier si un nombre est premier. Au cours des prochaines minutes, vous apprendrez à trouver la solution optimale à cette question.

Dans ce didacticiel, vous allez :

revoir les bases des nombres premiers,
écrire du code Python pour vérifier si un nombre est premier, et
l’optimiser davantage pour obtenir un algorithme de durée d’exécution O(√n).

Pour tout cela et bien plus encore, commençons.

Qu’est-ce qu’un nombre premier ?

Commençons par rappeler les principes de base des nombres premiers.

En théorie des nombres, un nombre naturel n est dit premier s’il a exactement deux facteurs: 1 et le nombre lui-même(n). Rappelez-vous les mathématiques de votre école : on dit qu’un nombre i est un facteur du nombre n, si i divise n de façon égale. ✅

Le tableau suivant énumère quelques nombres, tous leurs facteurs et indique s’ils sont premiers.

n	Facteurs	Est-il premier ?
1	1	Non
2	1, 2	Oui
3	1, 3	Oui
4	1, 2, 4	Non
7	1, 7	Oui
15	1, 3, 5, 15	Non

A partir du tableau ci-dessus, nous pouvons écrire ce qui suit :

2 est le plus petit nombre premier.
1 est un facteur de chaque nombre.
Tout nombre n est un facteur de lui-même.

Donc 1 et n sont des facteurs triviaux pour tout nombre n. Et un nombre premier ne doit pas avoir d’autres facteurs que ces deux-là.

Cela signifie que lorsque vous passez de 2 à n – 1, vous ne devriez pas être en mesure de trouver un facteur non trivial qui divise n sans reste.

Algorithme O(n) pour vérifier si un nombre est premier en Python

Dans cette section, nous allons formaliser l’approche ci-dessus dans une fonction Python.

Vous pouvez parcourir en boucle tous les nombres compris entre 2 et n – 1 à l’aide de l’objet range() de Python.

En Python, range(start, stop, step) renvoie un objet range. Vous pouvez ensuite itérer sur l’objet range pour obtenir une séquence allant de start à stop -1 par pas de step.

Puisque nous avons besoin de l’ensemble des entiers de 2 à n-1, nous pouvons spécifier range(2, n) et l’utiliser en conjonction avec la boucle for.

Voici ce que nous souhaitons faire :

Si vous trouvez un nombre qui divise n uniformément sans reste, vous pouvez immédiatement conclure que ce nombre n’est pas premier.

Si vous avez parcouru en boucle l’ensemble des nombres allant de 2 à n – 1 sans trouver de nombre qui divise n uniformément, alors le nombre est premier.

Fonction Python pour vérifier si un nombre est premier

Sur la base de ce qui précède, nous pouvons définir la fonction is_prime() comme suit.

def is_prime(n) :
  for i in range(2,n) :
    si (n%i) == 0 :
      return False
  return True

Analysons maintenant la définition de la fonction ci-dessus.

La fonction is_prime() ci-dessus prend un entier positif n comme argument.
Si vous trouvez un facteur dans l’intervalle spécifié (2, n-1), la fonction renvoie False, carle nombre n’est pas premier.
Elle renvoie également True si vous parcourez l’ensemble de la boucle sans trouver de facteur.

Ensuite, appelons la fonction avec des arguments et vérifions si la sortie est correcte.

is_prime(2)
# Vrai

is_prime(8)
# Faux

is_prime(9)
# Faux

is_prime(11)
# Vrai

Dans la sortie ci-dessus, vous voyez que 2 et 11 sont premiers (la fonction renvoie True). Et que 8 et 9 ne sont pas premiers (la fonction renvoie False).

Comment optimiser la fonction Python is_prime()

Nous pouvons effectuer une petite optimisation ici. Observez la liste des facteurs dans le tableau ci-dessous.

Nombre	Facteurs
6	1, 2, 3, 6
10	1, 2, 5, 10
18	1, 2, 3, 6, 9, 18

Nous constatons que le seul facteur de n supérieur à n/2 est n lui-même.

Cela signifie que vous n’avez pas besoin de boucler jusqu’à n – 1. Vous pouvez à la place exécuter la boucle jusqu’à n/2 seulement.

Si vous ne trouvez pas de facteur non trivial jusqu’à n/2, vous n’en trouverez pas non plus au-delà.

Modifions maintenant la fonction is_prime() pour qu’elle vérifie la présence de facteurs dans l’intervalle (2, n/2)

def is_prime(n) :
  for i in range(2,int(n/2)) :
    si (n%i) == 0 :
      return False
  return True

Vérifions le résultat à l’aide de quelques appels de fonction.

is_prime(9)
# Faux

is_prime(11)
# Vrai

Même s’il semble avoir été optimisé, cet algorithme n’est pas plus efficace que le précédent en termes de complexité d’exécution. En fait, les deux ont une complexité d’exécution O(n): proportionnelle à la valeur de n ou linéaire en n.

Peut-on faire mieux ? Oui, c’est possible !

▶️ Passez à la section suivante pour déterminer comment améliorer la complexité temporelle du test des nombres premiers.

Algorithme O(√n) pour vérifier les nombres premiers en Python

Il arrive que les facteurs d’un nombre se présentent par paires.

Si a est un facteur du nombre n, il existe également un facteur b tel que a x b = n, ou plus simplement, ab = n.

Vérifions cela à l’aide d’un exemple.

Le tableau ci-dessous montre les facteurs du nombre 18 apparaissant par paires. Vous pouvez vérifier la même chose pour d’autres nombres si vous le souhaitez.

Notez également que √18 est approximativement égal à 4,24.

Et dans les facteurs qui apparaissent par paires (a, b), vous pouvez voir que si a est inférieur à 4,24, alors b est supérieur à 4,24 – dans cet exemple, (2, 18) et (3, 6).

a	b
1	18
2	9
3	6

Facteurs de 18 par paires

La figure ci-dessous montre les facteurs de 18 sur la droite numérique.

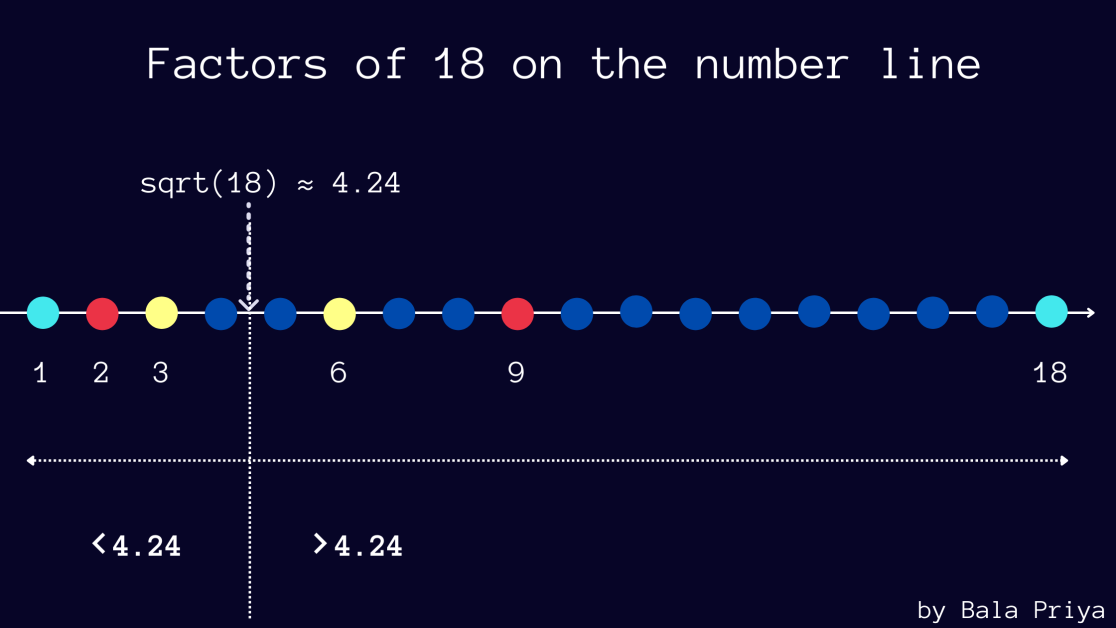
Si le nombre n est un carré parfait, vous aurez a = b = √n comme facteur.

▶️ Regardez les facteurs de 36 dans le tableau ci-dessous. Comme 36 est un carré parfait, a = b = 6 est l’un des facteurs. Pour toutes les autres paires de facteurs (a, b), a 6 sont valables.

a	b
1	36
2	18
3	12
4	9
6	6

Facteurs de 36 par paires

En résumé, nous avons ce qui suit :

Tout nombre n peut s’écrire sous la forme n = a x b
Si n est un carré parfait, alors a = b = √n.
Et si a < b, alors a < √n et b > √n.
Sinon, si a > b, alors a > √n et b < √n.

Ainsi, au lieu de parcourir en boucle tous les entiers jusqu’à n/2, vous pouvez choisir de le faire jusqu’à √n. Et c’est beaucoup plus efficace que notre approche précédente.

Comment modifier is_prime() en algorithme O(√n)

Procédons à l’optimisation de la fonction de vérification des nombres premiers en Python.


import math
def is_prime(n) :
  for i in range(2,int(math.sqrt(n)) 1) :
    si (n%i) == 0 :
      retour Faux
  return True

Analysons maintenant la définition de la fonction ci-dessus :

Pour calculer la racine carrée d’un nombre, importons le module mathématique intégré de Python et utilisons la fonction math.sqrt().
Comme n n ‘est peut-être pas un carré parfait, nous devons le convertir en un entier. Utilisez int(var) pour convertir var en un entier.
Pour nous assurer que nous vérifions bien jusqu’à √n, nous ajoutons un plus un, car la fonction range() exclut par défaut le point final de la plage.

La cellule de code ci-dessous vérifie que notre fonction is_prime() fonctionne correctement.

is_prime(8)
# Faux

is_prime(15)
# Faux

is_prime(23)
# Vrai

Dans la section suivante, nous allons créer quelques graphiques simples pour comprendre visuellement O(n) et O(√n).

Comparaison visuelle de O(n) et O(√n)

▶️ Exécutez l’extrait de code suivant dans l’environnement Jupyter Notebook de votre choix.

import numpy as np
import seaborn as sns
import pandas as pd


n = 20

x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1, "O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)

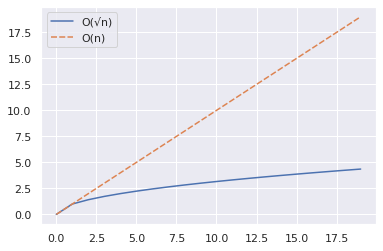
L’extrait ci-dessus montre comment vous pouvez tracer les courbes de n et √n pour une plage de valeurs.

Nous utilisons la fonction NumPy arange() pour créer un tableau de nombres.
Ensuite, nous rassemblons les valeurs de n et √n jusqu’à 20 inclus dans un DataFrame pandas.
Ensuite, nous traçons un graphique à l’aide de la fonction lineplot() de seaborn.

Le graphique ci-dessous montre que √n est significativement plus petit que n.

Augmentons maintenant la plage jusqu’à 2000 et répétons les mêmes étapes que ci-dessus.

import numpy as np
import seaborn as sns
import pandas as pd


n = 2000

x = np.arange(n)
y1 = np.sqrt(x)
y2 = x
df = pd.DataFrame({"O(√n)":y1, "O(n)":y2})
sns.set_theme()
sns.lineplot(data = df)

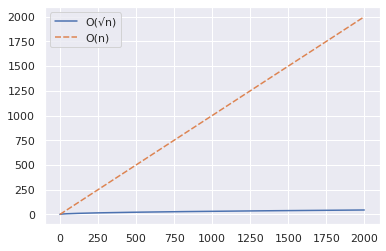
D’après le graphique ci-dessus, vous pouvez déduire que l’algorithme O(√n) est significativement plus rapide lorsque vous testez si un grand nombre est premier.

Voici un exemple rapide : 2377 est un nombre premier – vérifiez-le!😀

Alors que l’approche O(n) nécessite environ 2 000 étapes, l’algorithme O(√n) permet d’obtenir la réponse en seulement 49 étapes.✅

Conclusion

⏳ Il est temps de faire un rapide résumé.

Pour vérifier si un nombre est premier, l’approche naïve consiste à parcourir en boucle tous les nombres de l’intervalle (2, n-1). Si vous ne trouvez pas de facteur divisant n, alors n est premier.
Comme le seul facteur de n supérieur à n/2 est n lui-même, vous pouvez choisir de ne parcourir que n/2.
Les deux approches ci-dessus ont une complexité temporelle de O(n).
Comme les facteurs d’un nombre apparaissent par paires, vous pouvez choisir de n’exécuter que jusqu’à √n. Cet algorithme est beaucoup plus rapide que O(n). Et le gain est appréciable lorsqu’il s’agit de vérifier si un grand nombre est premier ou non.

J’espère que vous avez compris comment vérifier si un nombre est premier en Python. Pour la suite, vous pouvez consulter notre tutoriel sur les programmes Python sur les opérations sur les chaînes de caractères, oùvous apprendrez à vérifier si les chaînes de caractères sont des palindromes, des anagrammes, et plus encore.

Nous nous reverrons dans un autre tutoriel. D’ici là, bon codage!👩🏽‍💻

Bala Priya C
Contributeur
Bala Priya est une développeuse et rédactrice technique indienne qui a plus de trois ans d’expérience dans la rédaction de contenu technique. Elle partage ses connaissances avec la communauté des développeurs en rédigeant des tutoriels techniques, des guides pratiques, etc. Elle travaille actuellement comme rédactrice technique chez Geekflare. Elle contribue également activement à plusieurs autres publications techniques telles que freeCodeCamp et KDnuggets.