Ce tutoriel vous apprendra à utiliser NumPy linspace() pour créer un tableau de nombres régulièrement espacés en Python.
Vous apprendrez la syntaxe de NumPy linspace(), suivie d’exemples qui vous aideront à comprendre comment l’utiliser.
Remarque : pour suivre ce tutoriel, vous devez avoir installé Python et NumPy.
Vous n’avez pas encore NumPy ? Nous avons préparé un guide d’installation rapide pour vous.
C’est parti !
Installer et importer NumPy
Avant de commencer le tutoriel, passons rapidement en revue les étapes d’installation de la bibliothèque NumPy.
si vous avez déjà installé NumPy, vous pouvez passer à la section suivante.
- Si vous utilisez Google Colab – unenvironnement de bloc-notes Jupyter basé sur le cloud, vous pouvez importer NumPy et commencer à coder immédiatement. (recommandé pour ce tutoriel ✅)
- Si vous souhaitez mettre en place un environnement de travail local, je vous recommande d’installer la distribution Anaconda de Python. Anaconda est livré avec plusieurs paquets utiles préinstallés. Vous pouvez télécharger le programme d’installation correspondant à votre système d’exploitation. Le processus d’installation ne prend que quelques minutes
- Si Python est déjà installé sur votre ordinateur, vous pouvez toujours installer la distribution Anaconda. Vous pouvez utiliser conda ou pip pour installer et gérer les paquets. Vous pouvez exécuter l’une des commandes suivantes depuis l’invite de commande Anaconda pour installer NumPy.
# Installer NumPy en utilisant conda
conda install numpy
# Installez NumPy en utilisant pip
pip install numpyPour l’étape suivante, importez numpy sous l’alias np en exécutant la commande suivante. Cela vous permettra de référencer NumPy en tant que np, sansavoir à taper numpy à chaque fois que vous accédez à un élément du module.
import numpy as npÀ l’avenir, nous utiliserons la notation par points pour accéder à toutes les fonctions de la bibliothèque NumPy, comme ceci : np.<nom de la fonction>.
L’intérêt des nombres régulièrement espacés
Lorsque vous travaillez avec des tableaux NumPy, il arrive que vous ayez besoin de créer un tableau de nombres régulièrement espacés dans un intervalle.
Avant d’aller plus loin, passons rapidement en revue une autre fonction similaire , np.arange().
NumPy linspace() vs NumPy arange()
Si vous avez déjà utilisé NumPy, vous avez probablement utilisé np.arange() pour créer un tableau de nombres dans un intervalle spécifié.
Vous savez que
np.arange(start, stop, step)renvoie un tableau de nombres allant destartàstopinclus, par pas destep; la taille de pas par défaut étant 1.
Cependant, la valeur du pas n’est pas toujours évidente. Voyons pourquoi.
Par exemple, si vous avez besoin de 4 nombres régulièrement espacés entre 0 et 1, vous savez que la taille du pas doit être de 0,25. Mais si vous utilisez np.arange(), il n’inclut pas la valeur d’arrêt de 1. Vous devrez donc choisir un intervalle qui va au-delà de la valeur d’arrêt.
L’image suivante illustre quelques autres exemples dans lesquels vous avez besoin d’un nombre spécifique de points régulièrement espacés dans l’intervalle [a, b].
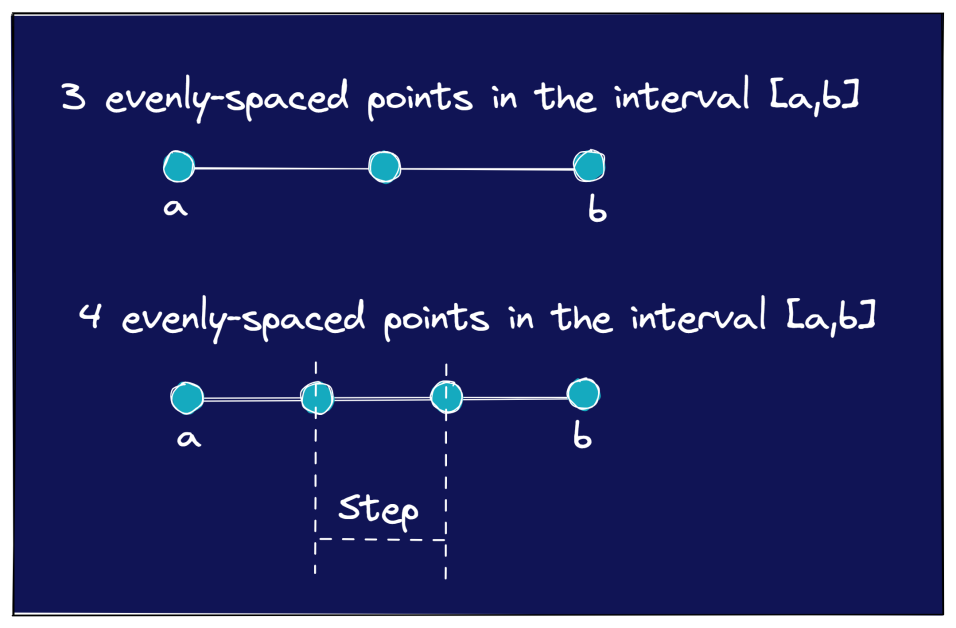
Notre premier exemple de 4 points régulièrement espacés dans [0,1] était assez facile. Vous savez que le pas entre les points doit être de 0,25.
Supposons que vous ayez un exemple un peu plus complexe, dans lequel vous devez énumérer 7 points régulièrement espacés entre 1 et 33. Dans ce cas, la taille du pas n’est peut-être pas très claire immédiatement. Vous pouvez toutefois calculer manuellement la valeur du pas dans ce cas.
Cependant, np.linspace() est là pour vous rendre la tâche encore plus simple ! 😄

Lorsque vous utilisez np.linspace(), vous n’avez qu’à spécifier le nombre de points dans l’intervalle – sans vous soucier de la taille du pas. Et vous obtiendrez le tableau comme vous le souhaitez.
Fort de cette motivation, nous allons apprendre la syntaxe de NumPy linspace() dans la section suivante.
Syntaxe de NumPy linspace()
La syntaxe d’utilisation de NumPy linspace() est présentée ci-dessous :
np.linspace(start, stop, num, endpoint, retstep, dtype, axis)Au départ, la syntaxe ci-dessus peut sembler très compliquée avec de nombreux paramètres.
Cependant, la plupart d’entre eux sont des paramètres optionnels, et nous arriverons à une syntaxe beaucoup plus simple dans quelques minutes.
Commençons par analyser la syntaxe ci-dessus :
startetstopsont respectivement les points de départ et d’arrivée de l’intervalle. Ces deux points peuvent être des scalaires ou des tableaux. Dans ce tutoriel, nous nous limiterons aux valeurs scalaires de début et de fin.numest le nombre de points régulièrement espacés. Il s’agit d’un paramètre facultatif dont la valeur par défaut est 50.endpointest également un paramètre facultatif qui peut prendre la valeur True ou False.- La valeur par défaut est True, ce qui signifie que le point final sera inclus dans l’intervalle par défaut. Toutefois, vous pouvez lui attribuer la valeur False pour exclure le point final.
retstepest un autre paramètre facultatif qui prend la valeur booléenne True ou False. Lorsqu’il vaut True, la valeur du pas est renvoyée.dtypeest le type de données des nombres du tableau. Le type est généralement déduit comme étant float et n’a pas besoin d’être fourni explicitement.axisest un autre paramètre facultatif indiquant l’axe le long duquel les nombres doivent être stockés. Ce paramètre n’est pertinent que lorsque les valeurs dedépartet d’arrêtsont elles-mêmes des tableaux.
▶️ Que retourne donc np.linspace()?
Il renvoie un tableau à N dimensions de nombres régulièrement espacés. Et si le paramètre retstep est défini sur True, il renvoie également la taille du pas.
Sur la base de ce qui a été dit jusqu’à présent, voici une syntaxe simplifiée pour utiliser np.linspace():
np.linspace(start, stop, num)La ligne de code ci-dessus renvoie un tableau de
numde nombres régulièrement espacés dans l’intervalle[start, stop].
Maintenant que vous connaissez la syntaxe, commençons à coder des exemples.
Comment créer des tableaux régulièrement espacés avec NumPy linspace()
#1. Pour notre premier exemple, créons un tableau de 20 nombres régulièrement espacés dans l’intervalle [1, 5].
Vous pouvez spécifier les valeurs de start, stop et num comme arguments de mot-clé. C’est ce que montre la cellule de code ci-dessous :
import numpy as np
arr1 = np.linspace(start = 1,stop = 5,num = 20)
print(arr1)
# Sortie :
[1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
4.78947368 5. ]
Remarquez que les nombres du tableau commencent à 1 et se terminent à 5, y compris les deux extrémités. Observez également comment les nombres, y compris les points 1 et 5, sont représentés comme des flottants dans le tableau retourné.
#2. Dans l’exemple précédent, vous avez passé les valeurs de start, stop et num comme arguments de mot-clé. Si vous passez les arguments dans le bon ordre, vous pouvez tout aussi bien les utiliser en tant qu’arguments positionnels avec seulement les valeurs, comme indiqué ci-dessous.
import numpy as np
arr2 = np.linspace(1,5,20)
print(arr2)
# Sortie :
[1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
4.78947368 5. ]#3. Créons maintenant un autre tableau dans lequel nous attribuons la valeur True à retstep.
Cela signifie que la fonction renverra à la fois le tableau et l’étape. Et nous pouvons les décompresser en deux variables arr3: le tableau, et step_size: la taille du pas retourné.
La cellule de code suivante explique comment procéder.
import numpy as np
arr3, step_size = np.linspace(1,5,20,retstep = True)
print(arr3)
# Sortie :
[1. 1.21052632 1.42105263 1.63157895 1.84210526 2.05263158
2.26315789 2.47368421 2.68421053 2.89473684 3.10526316 3.31578947
3.52631579 3.73684211 3.94736842 4.15789474 4.36842105 4.57894737
4.78947368 5. ]
# Sortie :
print(step_size)
0.21052631578947367#4. Comme dernier exemple, fixons la valeur de endpoint à False, et vérifions ce qui se passe.
import numpy as np
arr4 = np.linspace(1,5,20,endpoint = False)
print(arr4)
# Sortie :
[1. 1.2 1.4 1.6 1.8 2. 2.2 2.4 2.6 2.8 3. 3.2 3.4 3.6 3.8
4. 4.2 4.4 4.6 4.8]Dans le tableau retourné, vous pouvez voir que 1 est inclus, tandis que 5 n’est pas inclus. La dernière valeur du tableau est 4,8, mais nous avons encore 20 nombres.
Jusqu’à présent, nous n’avons généré que des tableaux de nombres régulièrement espacés. Dans la section suivante, nous allons visualiser ces nombres en les traçant.
Comment tracer des nombres régulièrement espacés dans un intervalle ?
Dans cette section, choisissons [10,15] comme intervalle d’intérêt. Ensuite, utilisez np.linspace() pour générer deux tableaux, chacun avec 8 et 12 points, respectivement.
Une fois cette opération terminée, nous pouvons utiliser la fonction plotting de la bibliothèque matplotlib pour les tracer.
Pour plus de clarté, nous serrerons les deux tableaux de N1 = 8 et N2 = 12 points régulièrement espacés à différentes positions le long de l’axe des ordonnées.
L’extrait de code suivant en fait la démonstration.
import numpy as np
import matplotlib.pyplot as plt
N1 = 8
N2 = 12
a = 10
b = 15
y1 = np.zeros(N1)
y2 = np.zeros(N2)
x1 = np.linspace(a, b, N1)
x2 = np.linspace(a, b, N2)
plt.plot(x1, y1-0.5, 'o')
plt.plot(x2, y2 0.5, 'o')
plt.ylim([-1, 1])
plt.title(f'Evenly Spaced Numbers in the Interval [{a},{b}]')
plt.xlabel('Interval')
plt.show()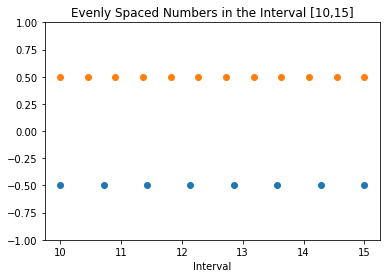
La génération de points régulièrement espacés peut s’avérer utile lorsque vous travaillez avec des fonctions mathématiques. Nous en apprendrons plus à ce sujet dans la section suivante.
Comment utiliser NumPy linspace() avec les fonctions mathématiques
Après avoir généré un tableau de nombres régulièrement espacés à l’aide de np.linspace(), vous pouvez calculer les valeurs des fonctions mathématiques dans l’intervalle.
Dans la cellule de code ci-dessous, vous commencez par générer 50 points régulièrement espacés dans l’intervalle 0 à 2π. Ensuite, vous créez le tableau y en utilisant np.sin() sur le tableau x. Notez que vous pouvez ignorer le paramètre num, car la valeur par défaut est 50. Nous l’utiliserons quand même explicitement.
L’étape suivante consiste à tracer la fonction sinus dans l’intervalle [0, 2π]. Pour ce faire, vous pouvez utiliser matplotlib, comme dans l’exemple précédent. Plus précisément, la fonction plot() de matplotlib.pytplot est utilisée pour créer un tracé linéaire.
import numpy as np
import matplotlib.pyplot as plt
N = 50
a = 0.0
b = 2*np.pi
x = np.linspace(a, b, N)
y = np.sin(x)
plt.plot(x, y, marker = "o")
plt.ylim([-1, 1])
plt.title(f'y = sin(x)')
plt.xlabel('x ---->
')
plt.show()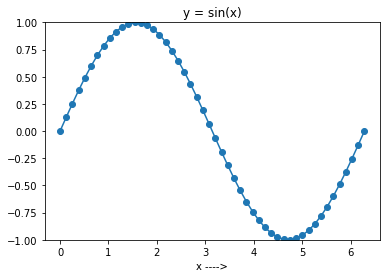
Maintenant, exécutez le code ci-dessus en réglant N sur 10. Vous obtiendrez le graphique illustré dans la figure ci-dessous.
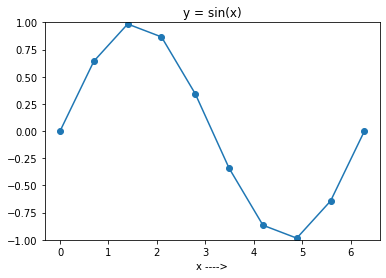
Vous pouvez constater que le tracé n’est pas très lisse, car vous n’avez choisi que 10 points dans l’intervalle.
En général, plus le nombre de points pris en compte est important, plus le tracé de la fonction sera lisse.
Conclusion
Voici un résumé de ce que nous avons appris.
- np.linspace(start, stop, num) renvoie un tableau de num de nombres régulièrement espacés dans l’intervalle [start, stop].
- Définissez le paramètre optionnel endpoint à False pour exclure stop, et définissez l’intervalle à [start, stop].
- Définissez facultativement retstep à True pour obtenir la taille du pas.
- Générez des tableaux régulièrement espacés à l’aide de np.linspace(), puis utilisez le tableau avec des fonctions mathématiques.
J’espère que vous comprenez maintenant comment fonctionne np.linspace(). Vous pouvez choisir d’exécuter les exemples ci-dessus dans le carnet Jupyter. Consultez notre guide sur le notebook Jupyter, ou d’autres alternatives à Jupyter que vous pouvez considérer.
À bientôt dans un autre tutoriel Python. D’ici là, continuez à coder!😀

